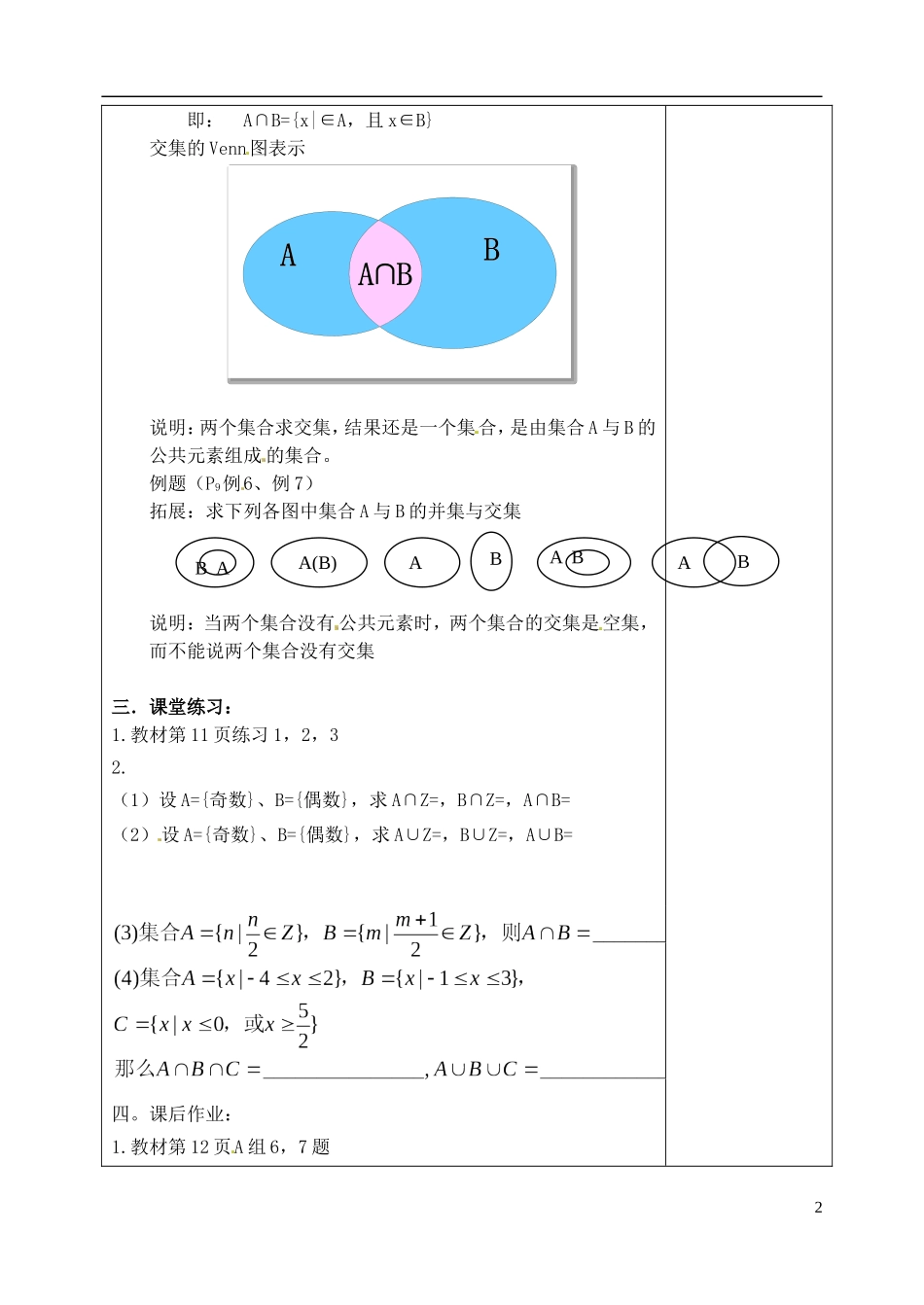
`1.1.3集合的基本运算(一)教学目标:(1)理解两个集合的并集与交集的的含义,会求两个简单集合的并集与交集;(2)能用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。教学重点:并集和交集的概念教学难点:集合的交集与并集的区别教学过程:一.引入:考察集合A={1,2,3},B={2,3,4}与集合C={1,2,3,4}之间的关系.二讲授新课:1.并集一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集记作:A∪B读作:“A并B”即:A∪B={x|x∈A,或x∈B}Venn图表示:说明:两个集合求并集,结果还是一个集合,是由集合A与B的所有元素组成的集合(重复元素只看成一个元素)。例题(P8例4、例5)说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。问题:在上图中我们除了研究集合A与B的并集外,它们的公共部分(即问号部分)还应是我们所关心的,我们称其为集合A与B的交集。2.交集一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集。记作:A∩B读作:“A交B”1AB∪AB∪ABA?即:A∩B={x|∈A,且x∈B}交集的Venn图表示说明:两个集合求交集,结果还是一个集合,是由集合A与B的公共元素组成的集合。例题(P9例6、例7)拓展:求下列各图中集合A与B的并集与交集说明:当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集三.课堂练习:1.教材第11页练习1,2,32.(1)设A={奇数}、B={偶数},求A∩Z=,B∩Z=,A∩B=(2)设A={奇数}、B={偶数},求A∪Z=,B∪Z=,A∪B=四。课后作业:1.教材第12页A组6,7题2ABA(B)ABBABA2.(选做)(1)已知X={x|x2+px+q=0,p2-4q>0},A={1,3,5,7,9},B={1,4,7,10},且,试求p、q;2.集合A={x|x2+px-2=0},B={x|x2-x+q=0},若AB={-2,0,1},求p、q;课后记:3