广东省广州育才中学高三数学 综合训练《立体几何中求角与距离》VIP免费

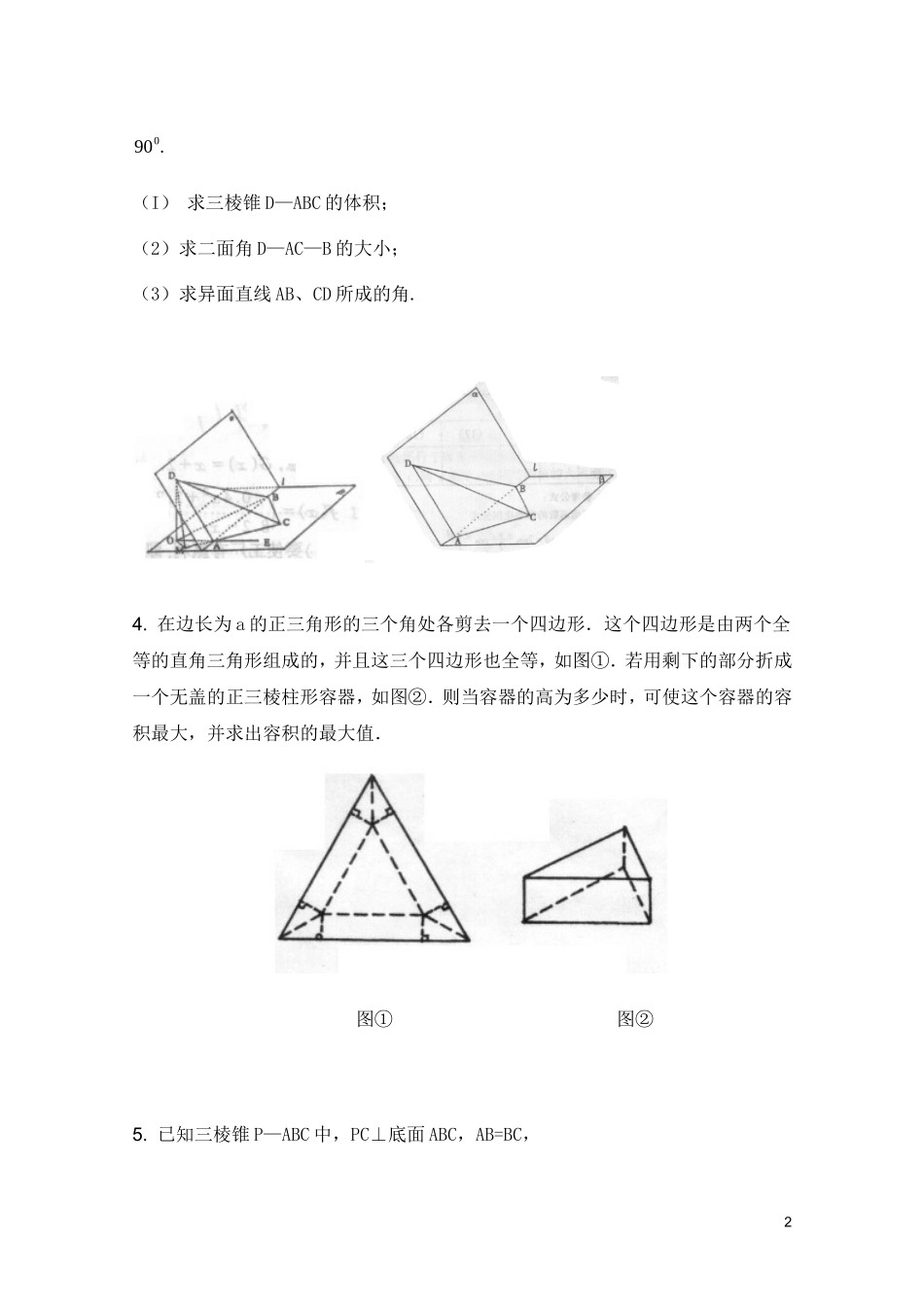
ABCDA1EB1C1广州育才中学高三数学各类题型综合训练系列立体几何中求角与距离1.四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD.（1）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；（2）证明无论四棱锥的高怎样变化，面PAD与面PCD所成的二面角恒大于90°2如图，直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形，∠ACB=900，AC=1，C点到AB1的距离为CE=23，D为AB的中点.（1）求证：AB1⊥平面CED；（2）求异面直线AB1与CD之间的距离；（3）求二面角B1—AC—B的平面角.3.如图a—l—是120°的二面角，A，B两点在棱上，AB=2，D在内，三角形ABD是等腰直角三角形，∠DAB=90°，C在内，ABC是等腰直角三角形∠ACB=1.900（I）求三棱锥D—ABC的体积；（2）求二面角D—AC—B的大小；（3）求异面直线AB、CD所成的角.4.在边长为a的正三角形的三个角处各剪去一个四边形．这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①．若用剩下的部分折成一个无盖的正三棱柱形容器，如图②．则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值．图①图②5.已知三棱锥P—ABC中，PC⊥底面ABC，AB=BC，2D、F分别为AC、PC的中点，DE⊥AP于E．（1）求证：AP⊥平面BDE；（2）求证：平面BDE⊥平面BDF；（3）若AE∶EP=1∶2，求截面BEF分三棱锥P—ABC所成两部分的体积比．6.如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F、G分别为EB和AB的中点.（1）求证：FD∥平面ABC；（2）求证：AF⊥BD；(3)求二面角B—FC—G的正切值.7.如图，正方体ABCD—A1B1C1D1的棱长为1，P、Q分别是线段AD1和BD上的点，且D1P∶PA=DQ∶QB=5∶12.(1)求证PQ∥平面CDD1C1；(2)求证PQ⊥AD；3ABCDEA1B1C1D1xyz图4(3)求线段PQ的长.8.如图4，在长方体ABCD1111ABCD中，AD=1AA=1，AB=2，点E在棱AB上移动。（Ⅰ）证明：11DEAD；（Ⅱ）当E为AB的中点时，求点E到面1ACD的距离；（Ⅲ）AE等于何值时，二面角1DECD的大小为4。9.如图，在正三棱柱ABC—A1B1C1中，各棱长都相等，D、E分别为AC1，BB1的中点。（1）求证：DE∥平面A1B1C1；（2）求二面角A1—DE—B1的大小。10．如图：已知直三棱柱ABC—A1B1C1，AB＝AC，F为棱BB1上一点，BF∶FB1＝2∶1，BF＝BC＝2a。（I）若D为BC的中点，E为AD上不同于A、D的任意一点，证明EF⊥FC1；4ABC1A1B1CED（II）试问：若AB＝2a，在线段AD上的E点能否使EF与平面BB1C1C成60°角，为什么？证明你的结论11.如图，在底面是直角梯形的四棱锥PABCD中，AD∥BC，∠ABC＝90°，且∠ADCarcsin55，又PA⊥平面ABCD，AD＝3AB＝3PA＝3a。（I）求二面角P—CD—A的正切值；（II）求点A到平面PBC的距离。PBCAD12.在直三棱柱ABC—A1B1C1中，CA=CB=CC1=2，∠ACB=90°，E、F分别是BA、BC的中点，G是AA1上一点，且AC1⊥EG.（Ⅰ）确定点G的位置；（Ⅱ）求直线AC1与平面EFG所成角θ的大小.13.已知四棱锥P—ABCD，底面ABCD是菱形，PDDAB,60平面ABCD，PD=AD，5点E为AB中点，点F为PD中点.（1）证明平面PED⊥平面PAB；（2）求二面角P—AB—F的平面角的余弦值14.在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小（结果用反三角函数值表示）；(Ⅱ)设O点在平面D1AP上的射影是H，求证：D1H⊥AP；(Ⅲ)求点P到平面ABD1的距离.15.如图，在四棱锥中，底面ABCD是正方形，侧棱底面ABCD，，E是PC的中点，作交PB于点F。(I)证明平面；(II)证明平面EFD；(III)求二面角的大小。16.如图，在棱长为1的正方体ABCD—A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点.6·B1PACDA1C1D1BOH·（I）试确定点F的位置，使得D1E⊥平面AB1F；（II）当D1E⊥平面AB1F时，求二面角C1—EF—A的大小（结果用反三角函数值表示）.17.如图，直四棱柱ABCD-A1B1C1D1的底面是梯形，AB∥CD，AD⊥DC，CD=2，DD1=AB=1，P、Q分别是CC1、C1D1的中点。点P到直线AD1的距离为223⑴求证：AC∥平面BPQ⑵求二面角B-PQ-D的大小18.已知长方体ABCD—A1B1C1D1中，AB=BC=4，AA1=8，E、F分别为AD和CC1的中点，O...