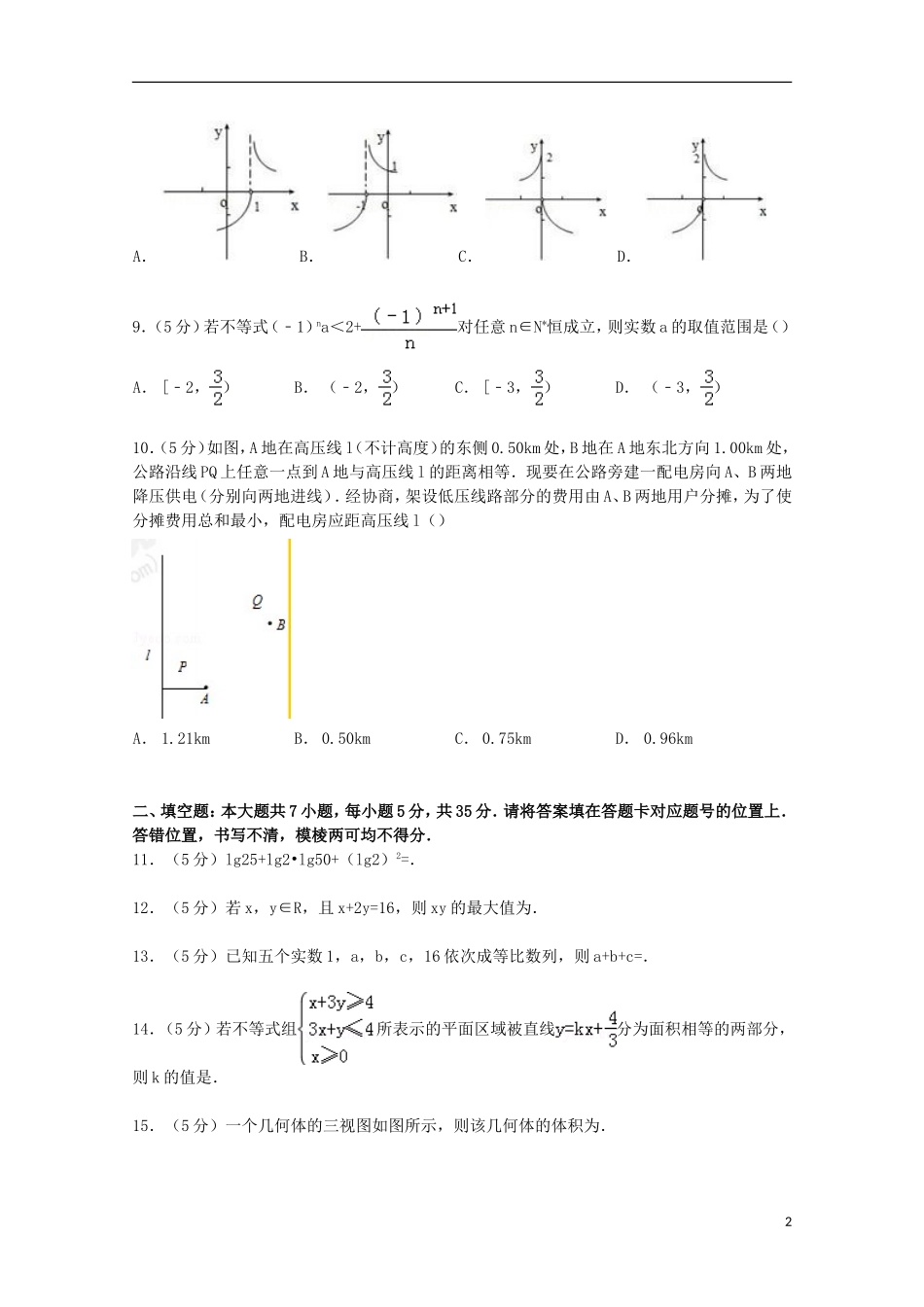
湖北省武汉市华中师大第一附中2015届高三上学期期中数学试卷(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件2.(5分)等差数列{an}中,若a4+a6+a8+a10+a12=120,则S15的值为()A.180B.240C.360D.7203.(5分)已知圆的方程为x2+y2﹣6x﹣8y=0.设该圆过点(﹣1,4)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.15B.30C.45D.604.(5分)若l,m,n是互不相同的空间直线,α,β是不重合的平面,下列命题正确的是()A.若α∥β,l⊂α,n⊂β,则l∥nB.若α⊥β,l⊂α,则l⊥βC.若l⊥n,m⊥n,则l∥mD.若l⊥α,l∥β,则α⊥β5.(5分)已知向量=(2,3),=(﹣1,2),若m+n与﹣2共线,则等于()A.﹣B.C.﹣2D.26.(5分)偶函数f(x)(x∈R)满足:f(﹣4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为()A.(﹣∞,﹣4)∪(4,+∞)B.(﹣4,﹣1)∪(1,4)C.(﹣∞,﹣4)∪(﹣1,0)D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4)7.(5分)若sin(﹣θ)=,则cos(+2θ)=()A.﹣B.﹣C.D.8.(5分)已知函数,则函数y=f(1﹣x)的图象是()1A.B.C.D.9.(5分)若不等式(﹣1)na<2+对任意n∈N*恒成立,则实数a的取值范围是()A.[﹣2,)B.(﹣2,)C.[﹣3,)D.(﹣3,)10.(5分)如图,A地在高压线l(不计高度)的东侧0.50km处,B地在A地东北方向1.00km处,公路沿线PQ上任意一点到A地与高压线l的距离相等.现要在公路旁建一配电房向A、B两地降压供电(分别向两地进线).经协商,架设低压线路部分的费用由A、B两地用户分摊,为了使分摊费用总和最小,配电房应距高压线l()A.1.21kmB.0.50kmC.0.75kmD.0.96km二、填空题:本大题共7小题,每小题5分,共35分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.11.(5分)lg25+lg2•lg50+(lg2)2=.12.(5分)若x,y∈R,且x+2y=16,则xy的最大值为.13.(5分)已知五个实数1,a,b,c,16依次成等比数列,则a+b+c=.14.(5分)若不等式组所表示的平面区域被直线分为面积相等的两部分,则k的值是.15.(5分)一个几何体的三视图如图所示,则该几何体的体积为.216.(5分)把边长为1的正方形ABCD如图放置,A、D别在x轴、y轴的非负半轴上滑动.(1)当A点与原点重合时,•=;(2)•的最大值是.17.(5分)用[x]表示不超过x的最大整数,例如[﹣2.5]=﹣3,[2.5]=2,设函数f(x)=[x[x]].(1)f(3.6)=;(2)若函数f(x)的定义域是[0,n),n∈N+,则其值域中元素个数为.三、解答题:本大题共5小题,共65分.解答应写出文字说明、证明过程或演算步骤.18.(12分)已知函数f(x)=sin2x﹣2cos2x++a.(1)求函数f(x)的单调递减区间;(2)设x∈[0,]时,f(x)的最小值是﹣2,求f(x)的最大值.19.(12分)如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,ABCD是矩形,E是棱PD的中点,PA=AD=4,AB=3.(1)证明PB∥底面ACE;(2)求直线PB与平面PAC所成角的正弦值.320.(13分)若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意正整数n,有an=﹣,4Tn﹣12Sn=13n.(1)求数列{bn}的通项公式;(2)设cn=bn+,若++…+>,求n的最小值.21.(14分)已知椭圆的中心为原点,焦点在x轴上,离心率为,且经过点M(4,1),直线l:y=x+m交椭圆于异于M的不同两点A,B.直线MA、MB与x轴分别交于点E、F.(1)求椭圆标准方程;(2)求m的取值范围;(3)证明△MEF是等腰三角形.22.(14分)已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x﹣2y﹣2=0.(1)求f(x)的解析式;(2)当x>1时,f(x)+<0恒成立,求实数k的取值范围;(3)设n是正整数,用n!表示前n个正整数的积,即n!=1•2•3…n.求证:n!<e.湖北省武汉市华中师大第一附中2015届高三上学...