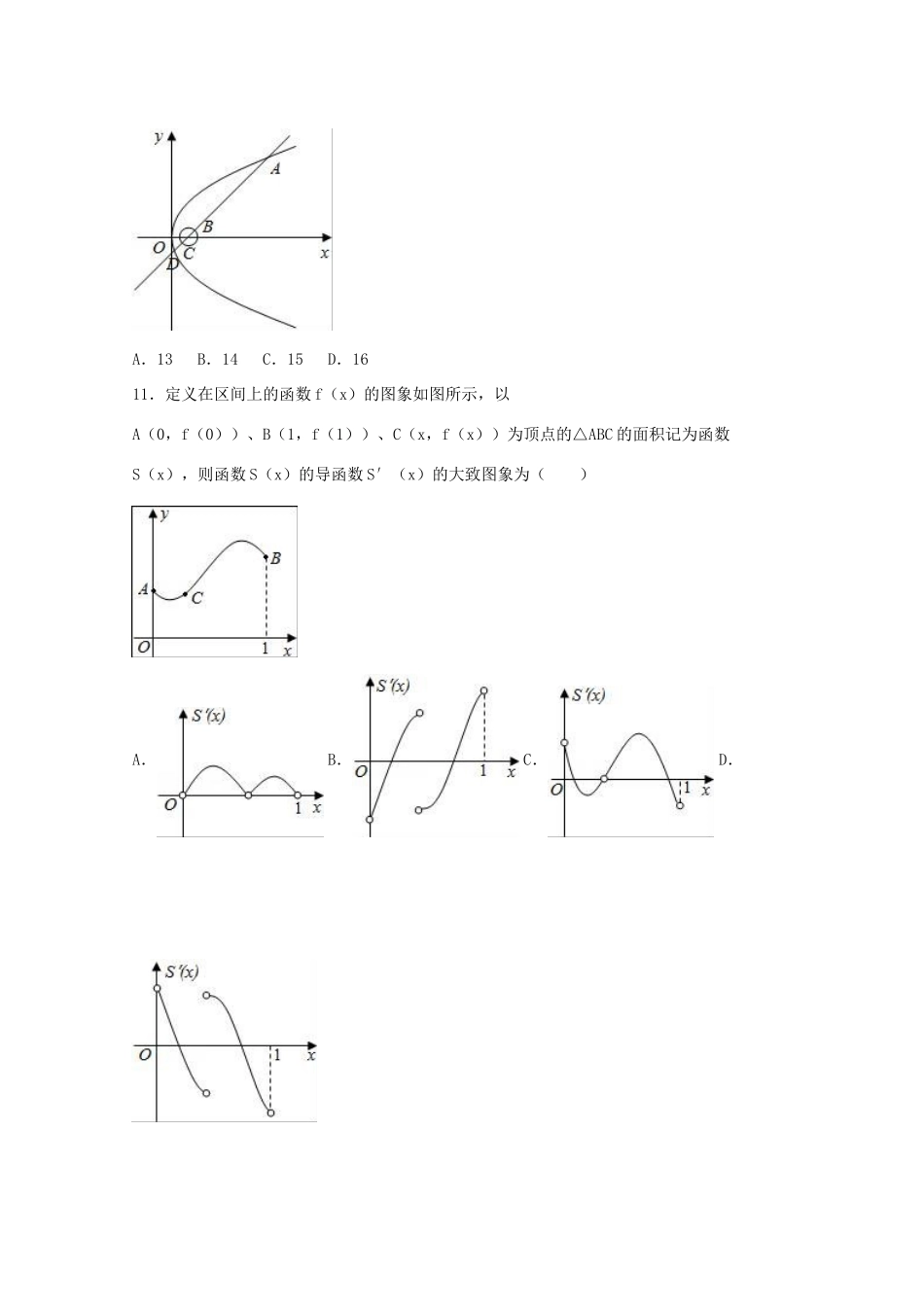
2016年河南省郑州一中高考数学冲刺卷(文科)(3)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,两共轭复数所对应的点()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称2.已知集合A={x|x≤1},若B⊆A,则集合B可以是()A.{x|x≤2}B.{x|x>1}C.{x|x≤0}D.R3.某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次输入的值为8,则第三次输出的值为()A.8B.15C.29D.364.具有线性相关关系得变量x,y,满足一组数据如表所示,若y与x的回归直线方程为=3x﹣,则m的值()x0123y﹣11m8A.4B.C.5D.65.已知x,y满足不等式组,则目标函数z=3x+y的最大值为()A.12B.24C.8D.6.已知两个单位向量的夹角为45°,且满足⊥(λ﹣),则实数λ的值为()A.1B.C.D.27.某三棱锥的侧视图和俯视图如图所示,则该三棱锥的体积为()A.4B.8C.12D.248.等差数列x1,x2,x3…x9的公差为1,若以上述数据x1,x2,x3…x9为样本,则此样本的方差为()A.B.C.60D.309.已知F是双曲线的右焦点,O为坐标原点,设P是双曲线C上一点,则∠POF的大小不可能是()A.15°B.25°C.60°D.165°10.如图,直线y=x﹣2与圆x2+y2﹣4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=()A.13B.14C.15D.1611.定义在区间上的函数f(x)的图象如图所示,以A(0,f(0))、B(1,f(1))、C(x,f(x))为顶点的△ABC的面积记为函数S(x),则函数S(x)的导函数S′(x)的大致图象为()A.B.C.D.12.已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=,若关于x的方程52﹣(5a+6)f(x)+6a=0(a∈R),有且仅有6个不同实数根,则实数a的取值范围是()A.0<a<1或a=B.0≤a≤1或a=C.0<a≤1或a=D.1<a≤或a=0二、填空题(每题5分,满分20分,将答案填在答题纸上)13.函数y=x+(x>1)的最小值是.14.将函数f(x)=cosx的图象向右平移个单位,得到函数y=g(x)的图象,则g()=.15.已知a,b,c分别为△ABC三个内角A,B,C的对边,若a2=b2+c2﹣bc,=+,则tanB=.16.已知数集A={a1,a2,a3,a4,a5}(0≤a1<a2<a3<a4<a5)具有性质p:对任意i,j∈Z,其中1≤i≤j≤5,均有(aj﹣ai)∈A,若a5=60,则a3=.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设数列{an}的前n项和为Sn,且Sn=2an﹣1(n=1,2,…).(Ⅰ)求数列{an}的通项公式;(Ⅱ)若数列{bn}满足bn+1=an+bn(n=1,2,…),b1=2,求数列{bn}的通项公式.18.“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下2×2列联表:接受挑战不接受挑战合计男性451560女性251540合计7030100根据表中数据,能否在犯错误的概率不超过0.1的前提下认为“冰桶挑战赛与受邀者的性别有关”?附:P(K2≥k0)0.1000.0500.0100.001k02.7063.8416.63510.82819.如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,==2.(Ⅰ)求证:平面MNO∥平面PAD;(Ⅱ)若平面PA⊥平面ABCD,∠PDA=60°,且PD=DC=BC=2,求几何体M﹣ABC的体积.20.已知中心在原点O,左右焦点分别为F1,F2的椭圆的离心率为,焦距为2,A,B是椭圆上两点.(1)若直线AB与以原点为圆心的圆相切,且OA⊥OB,求此圆的方程;(2)动点P满足:=+3,直线OA与OB的斜率的乘积为﹣,求动点P的轨...