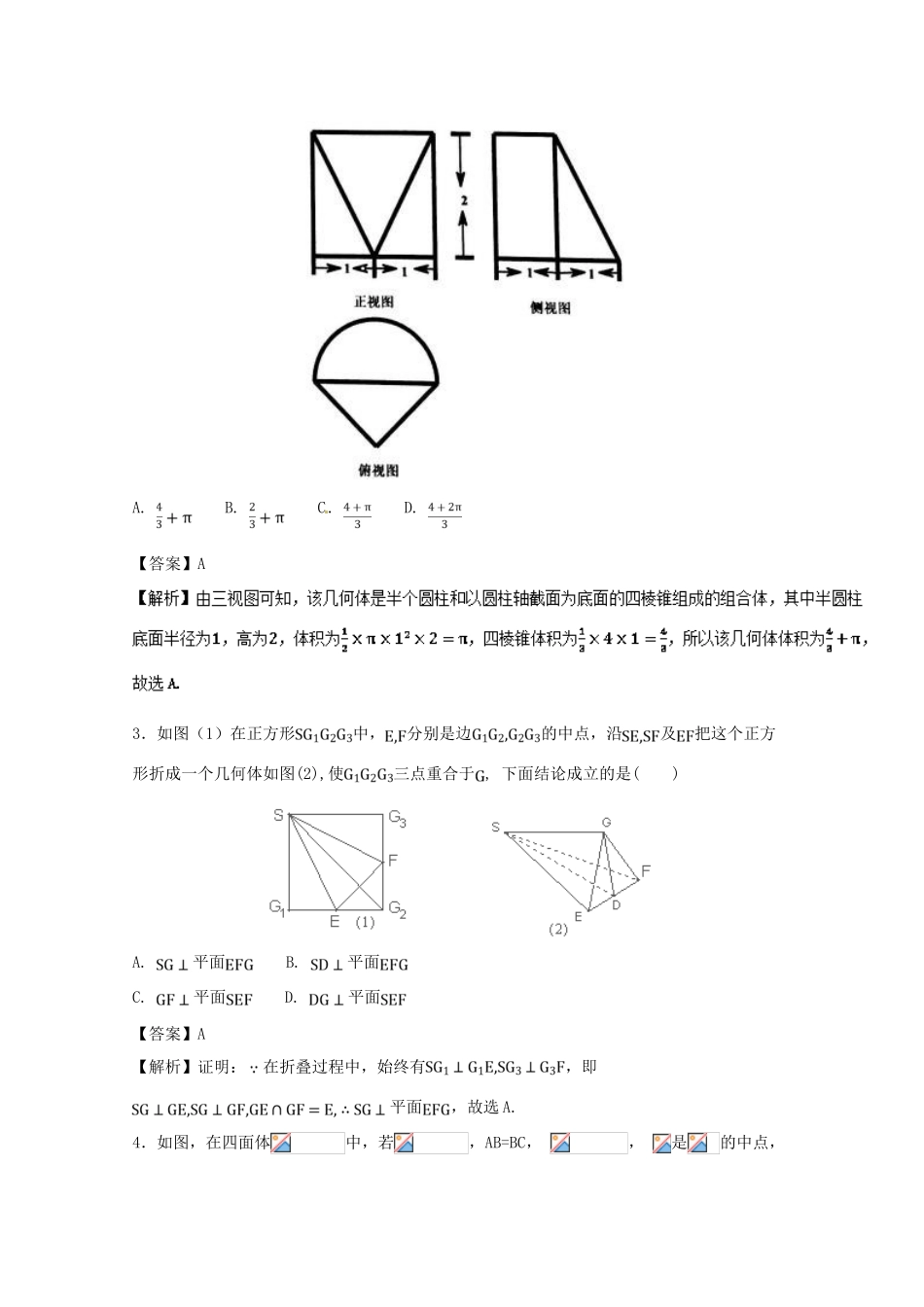
十一、立体几何角的计算与证明一、选择题1.【2017年浙江卷】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:)是A.B.C.D.【答案】A2.【2018届浙江省温州市高三9月测试(一模)】某几何体的三视图如图所示,则该几何体的体积(单位:)是()A.B.C.D.【答案】A3.如图(1)在正方形中,分别是边的中点,沿及把这个正方形折成一个几何体如图(2),使三点重合于,下面结论成立的是()A.平面B.平面C.平面D.平面【答案】A【解析】证明:在折叠过程中,始终有,即平面,故选A.4.如图,在四面体中,若,AB=BC,,是的中点,则下列命题中正确的是()A.平面平面B.平面平面C.平面平面,且平面平面D.平面平面,且平面平面【答案】C【解析】因为,,是的中点,⇒平面,由面面垂直判定定理可得平面平面,平面平面,故选C.5.已知正方体,点,,分别是线段,和上的动点,观察直线与,与.给出下列结论:①对于任意给定的点,存在点,使得;②对于任意给定的点,存在点,使得;③对于任意给定的点,存在点,使得;④对于任意给定的点,存在点,使得.其中正确结论的个数是().A.个B.个C.个D.个【答案】C②当点与重合时,且,∴平面, 对于任意给定的点,存在点,使得,故②正确.③只有垂直于在平面中的射影时,,故③正确.④只有平面时,④才正确,因为过点的平面的垂线与无交点,故④错误.综上,正确的结论是②③,故选.6.在正三棱柱中,,点、分别是棱、的中点,若,则侧棱的长为().A.B.C.D.【答案】B【解析】7.【2018届江西省南昌市高三上摸底】已知三棱锥的所有顶点都在球的球面上,满足,为球的直径且,则点到底面的距离为A.B.C.D.【答案】B【解析】 三棱锥的所有顶点都在球的球面上,为球的直径且,∴球心是的中点,球半径,过作平面,垂足是, 满足,,∴是中点,且,∴,∴点到底面的距离为,故选B.8.【2017届广东省广州高三下第一次模拟】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥为鳖臑,平面,,,三棱锥的四个顶点都在球的球面上,则球的表面积为().A.B.C.D.【答案】C9.【2018届海南省八校高三上新起点联考】在三棱锥中,,,,则异面直线与所成角的余弦值为()A.B.C.D.【答案】A【解析】10.【2017年浙江省镇海市镇海中学高中数学竞赛模拟(二)】如图,在四面体中,已知两两互相垂直,且.则在该四面体表面上与点距离为的点形成的曲线段的总长度为()A.B.C.D.【答案】B【解析】如图,设(在上,在上,在上).由,,知,,.∴在面内与点距离为的点形成的曲线段(图中弧)长为.同理,在面内与点距离为的点形成的曲线段长为.同理,在面内与点距离为的点形成的曲线段长为.同理,在面内与点距离为的点形成的曲线段长为.所以,该四面体表面上与点距离为的点形成的曲线段的总长度为.故选B.11.【2017届陕西省西安市西北工业大学附属中学高三下第八次模拟】已知正方体的棱长为2,其表面上的动点到底面的中心的距离为,则线段的中点的轨迹长度为()A.B.C.D.【答案】B12.【2018届辽宁省庄河市高级中学高三上开学】已知三棱锥的四个顶点都在同一个球面上,底面满足,若该三棱锥体积最大值为3,则其外接球的表面积为()A.B.C.D.【答案】D【解析】二、填空题13.【2018届浙江省名校协作体高三上学期考试】一个棱长为2的正方体被一个平面截去一部分后,剩下部分的三视图如下图所示,则该几何体的表面积为____________,体积为_________.【答案】【解析】:由三视图可知几何体是正方体在一个角上截去一个三棱锥, 正方体的棱长是2,∴三棱锥的体积,∴剩余部分体积,截面为边长为的正三角形,其面积为则该几何体的表面积为.14.在正三棱锥中,是的中点,且,底面边长,则正三棱锥的体积为__________,其外接球的表面积为__________.【答案】,15.【2017届浙江省杭州高级中学高三2月高考模拟】如图,正四面体的顶点在平面内,且直线与平面所成角为,顶点在平面上的射影为点,当顶点与点的距离最大时,直线与平面所成角的正弦值为__________.【答案】【解析】...