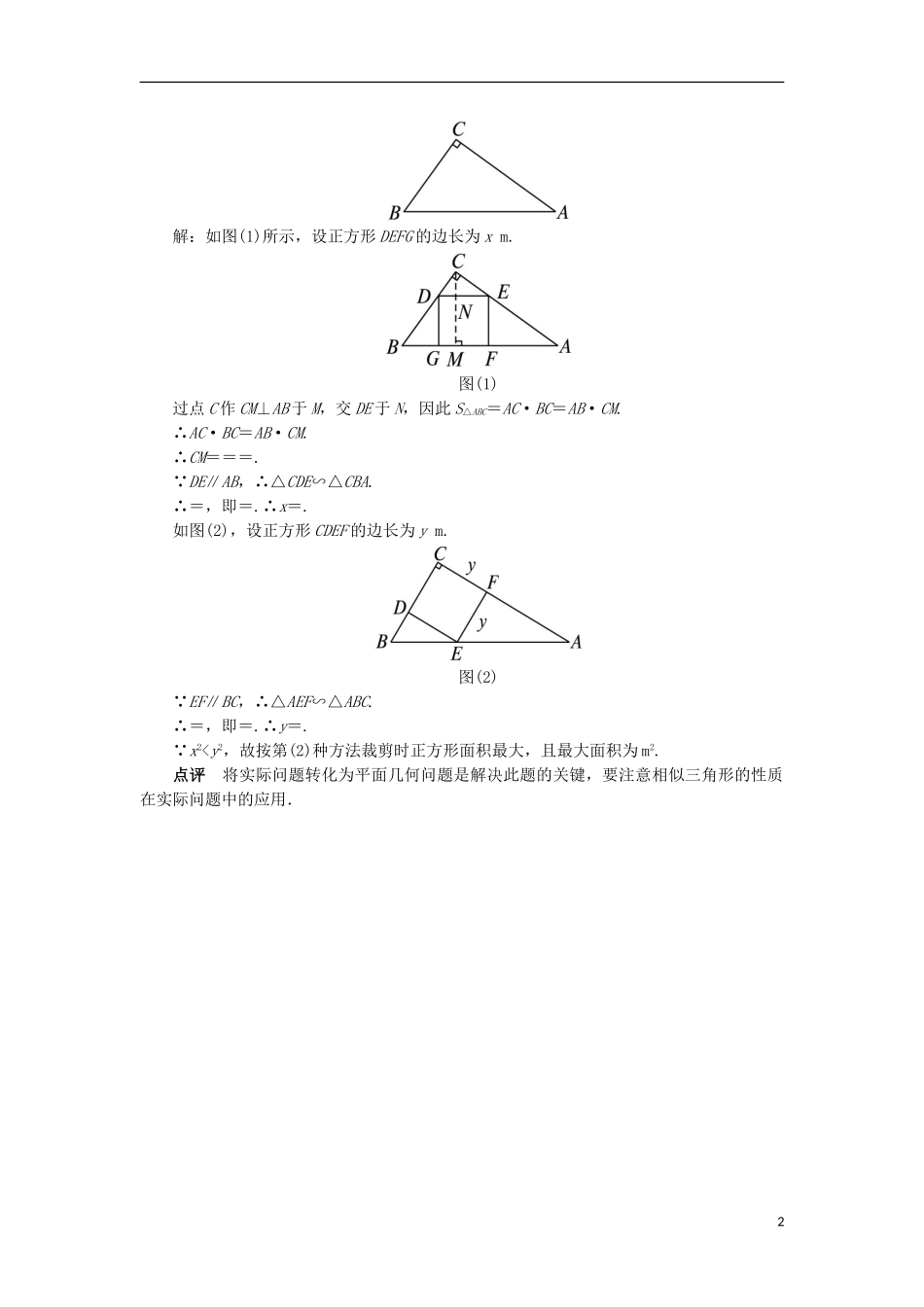
三相似三角形的判定及性质课堂探究探究一相似的问题在相似三角形中,与相似比相等的有:对应高的比,对应中线的比,对应角平分线的比、周长的比,外接(内切)圆的半径比、直径比、周长比,常利用比相等列方程来解决问题.【典型例题1】已知△ABC∽△A′B′C′,△ABC的周长为60cm,△A′B′C′的周长为72cm,AB=15cm,B′C′=24cm,求:(1)BC,A′B′;(2)AC,A′C′.思路分析:由周长的比得到相似比,再利用相似比解决.解:∵△ABC∽△A′B′C′,∴===.(1)∵AB=15cm,∴=,∴A′B′=18cm.∵B′C′=24cm,∴=,∴BC=20cm.(2)∵AB+BC+AC=60cm,∴AC=60-AB-BC=60-15-20=25(cm).同理可得A′C′=30cm.点评根据题意,利用相似三角形的周长之比等于相似比来求解.探究二面积比问题转化思想在数学解题中有着广泛的应用,关键是利用转化思想把三角形的面积比与相似比进行转化.【典型例题2】如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于点E,EF∥AB且交BC于点F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于多少?思路分析:由平行关系推导出△ADE∽△EFC,根据面积比得到对应边的比,再利用相似比转化解决.解:因为AD∥EF,DE∥FC,所以△ADE∽△ABC,△EFC∽△ABC,所以△ADE∽△EFC.又因为S△ADE∶S△EFC=1∶4,所以AE∶EC=1∶2.所以AE∶AC=1∶3.所以S△ADE∶S△ABC=1∶9.因为S△ADE=1,所以S△ABC=9.所以S四边形BFED=S△ABC-S△ADE-S△EFC=9-1-4=4.探究三实际应用问题此类问题是利用数学模型解实际问题,关键在于认真分析题意转化成数学问题,构造相似三角形求解.【典型例题3】如图所示,已知一块直角三角形木板的三边AB=5m,BC=3m,AC=4m,一加工车间要把它加工成一块面积最大的正方形木板.如何设计才能使木板的面积最大,并求出最大面积.1解:如图(1)所示,设正方形DEFG的边长为xm.图(1)过点C作CM⊥AB于M,交DE于N,因此S△ABC=AC·BC=AB·CM.∴AC·BC=AB·CM.∴CM===.∵DE∥AB,∴△CDE∽△CBA.∴=,即=.∴x=.如图(2),设正方形CDEF的边长为ym.图(2)∵EF∥BC,∴△AEF∽△ABC.∴=,即=.∴y=.∵x2