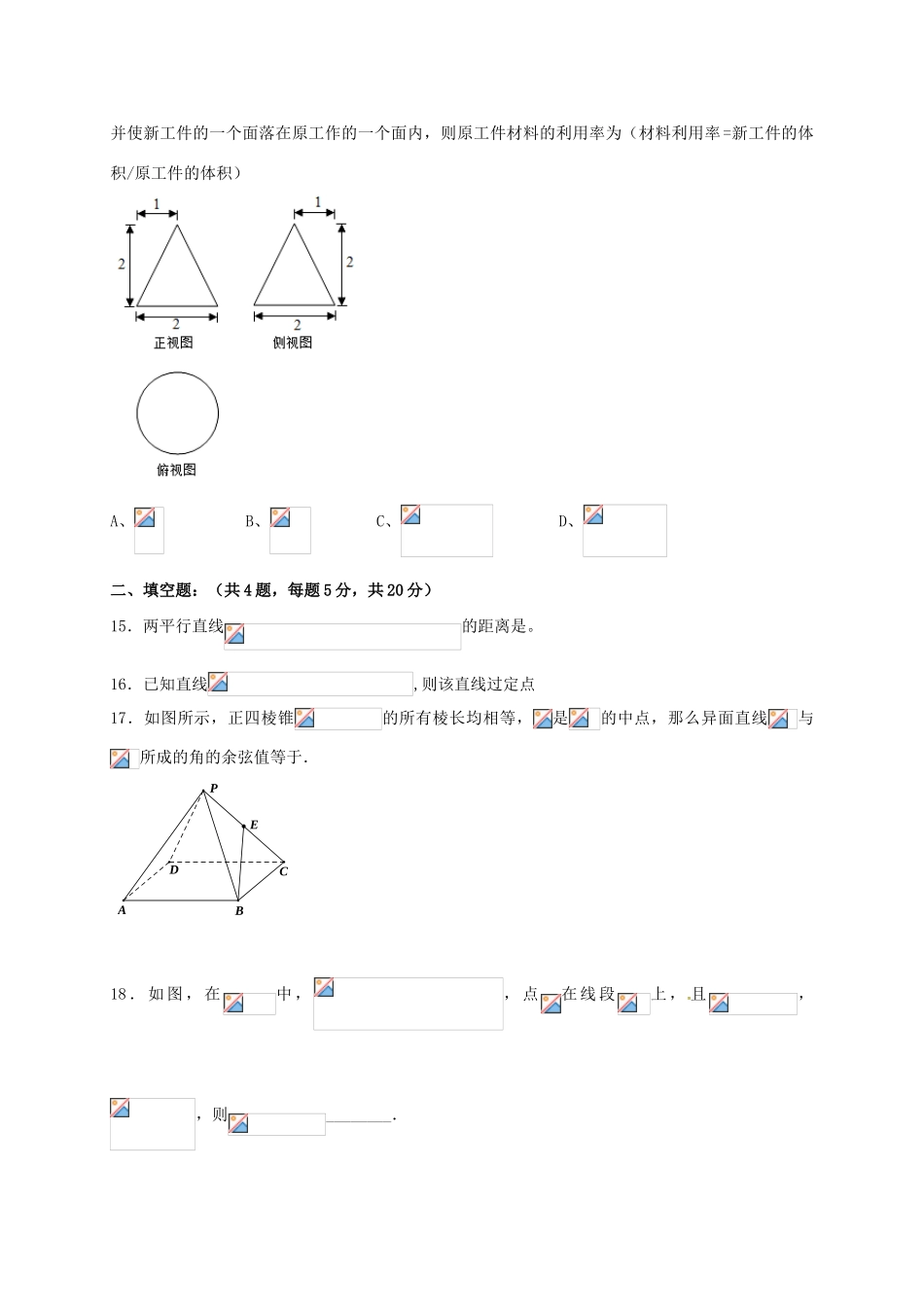
高一年级2016~2017学年度下学期期末考试数学(理)试题一、选择题:(共14题,每题5分,共70分,每题只有一个正确答案)1.已知等差数列的前项和为,若,则()A.B.C.D.2.直线,直线,若//,则等于()A.-3B.2C.-3或2D.3或-23.在等比数列中,则A.B.C.D.4.能保证直线与平面平行的条件是()A.直线与平面内的一条直线平行B.直线与平面内的某条直线不相交C.直线与平面内的无数条直线平行D.直线与平面内的所有直线不相交5.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B﹣AC﹣D,则四面体ABCD的外接球的体积为()A.πB.πC.πD.π6.一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为()A.B.C.D.7.在△ABC中,若a、b、c成等比数例,且c=2a,则cosB等于()A.B.C.D.8.正方体-中,与平面所成角的余弦值为()A.B.C.D.9.若,则下列不等式成立的是()A.B.C.D.10.若实数满足,则的取值范围为()A.B.C.D.11.设直线l的方程为:(),则直线l的倾斜角α的范围是A.B.C.D.12.中国古代数学著《九章算术》中记载了公元前年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若取,其几何体体积为(立方寸),则图中的为()A.B.C.D.13.在△ABC中,内角A,B,C对边的边长分别为为锐角,,则为()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形14.某工作的三视图如图所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)A、B、C、D、二、填空题:(共4题,每题5分,共20分)15.两平行直线的距离是。16.已知直线,则该直线过定点17.如图所示,正四棱锥的所有棱长均相等,是的中点,那么异面直线与所成的角的余弦值等于.ECDPAB18.如图,在中,,点在线段上,且,,则________.三、解答题:(共5题,每题12分,共60分)19.解下列关于的不等式:①;②.20.已知分别为三个内角的对边,.(1)求;(2)若,求的面积.21.已知直线经过点A,求:(1)直线在两坐标轴上的截距相等的直线方程;(2)直线与两坐标轴的正半轴围成三角形面积最小时的直线方程.22.如图,四边形与均为菱形,,且.(1)求证:平面;(2)求证:平面;(3)求二面角的余弦值.23.已知数列的前项和(为正整数)(1)令,求证数列是等差数列,并求数列的通项公式;(2)令,,试比较与的大小,并予以证明参考答案1.D2.A3.A4.D5.C6.B7.B8.A9.D10.B11.C12.D13.D14.A15.16.(-2,1)17.18.19.①解:且.…………………………………4分②解:原不等式化为:①当时,其解集为:;②当时,其解集为:;③当时,其解集为:或;④当时,其解集为:或;⑤当时,其解集为:.………………………………12分20.(1);(2).(1)由正弦定理化简已知等式,利用三角和内角和定理及三角函数恒等变换的应用化简可得;(2)由余弦定理可得,利用均值不等式可得,套用面积公式即可求解.(1)……2分…4分即,又,即……6分(2),……8分,即又由题意知.(当时等式成立)……10分……12分21.(1)当直线过原点时,方程为y=3x,当直线不过原点时,设直线的方程为:x+y=k,把点(1,3)代入直线的方程可得k值,即得所求的直线方程;(2)设直线方程为:,根据三角形的面积公式和基本不等式即可求出最值,继而得到直线方程22.(1)由线面垂直的判定定理得到结论;(2)通过证明线线平行,得到线面平行;(3)建立空间直角坐标系,求出平面的法向量,易知面,所以面的法向量为,再求出它们的夹角的余弦值.试题解析:(1)证明:设与相交于点,连接,因为四边形为菱形,所以,且为中点,又,所以,因为,所以平面.(2)证明:因为四边形与均为菱形,所以,,所以平面平面,又平面,所以平面.(3)解:因为四边形为菱形,且,所以△为等边三角形,因为为中点,所以,故平面.由,,两两垂直,建立如图所示的空间直角坐标系.设,因为四边形为菱形,,则,...