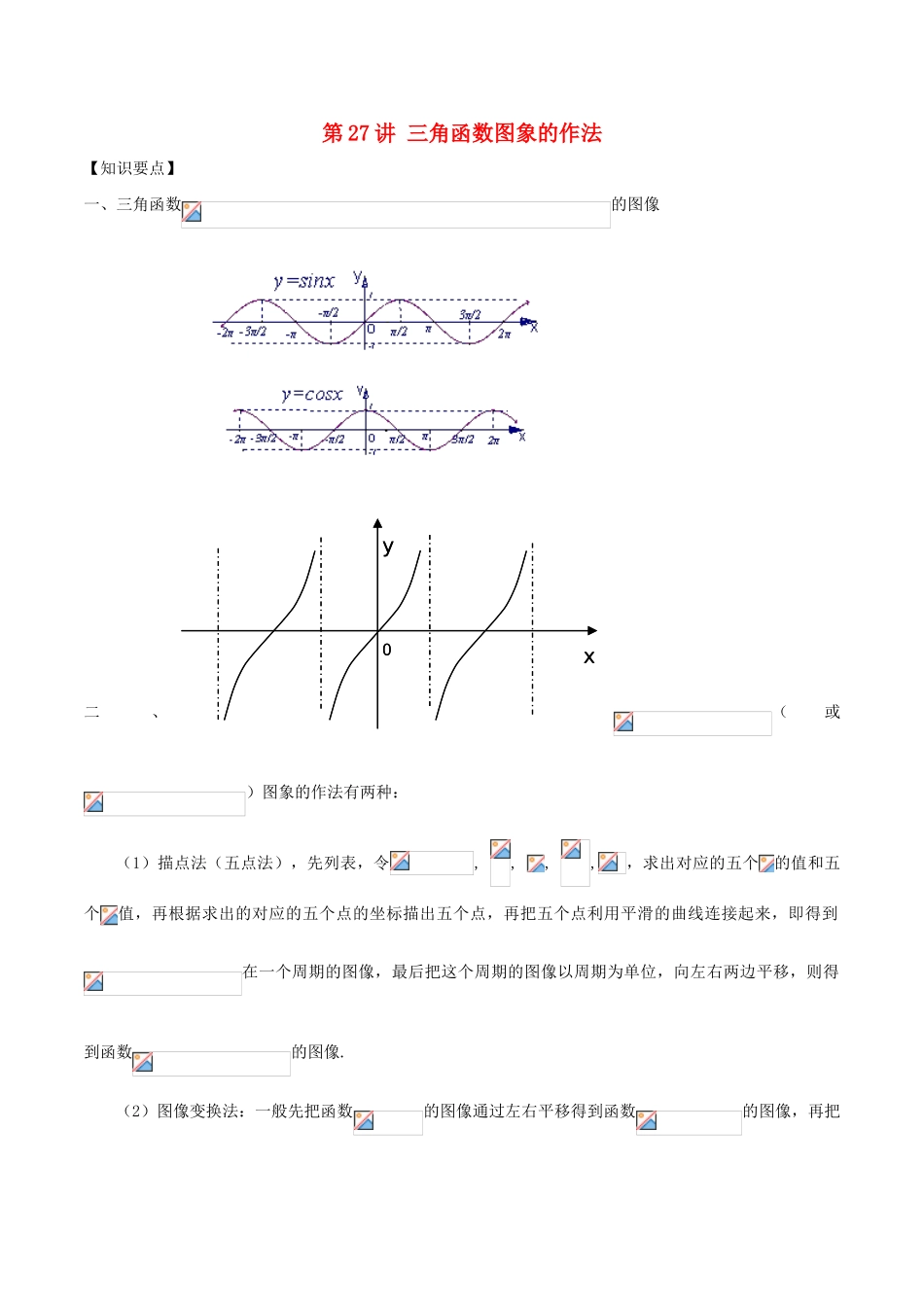
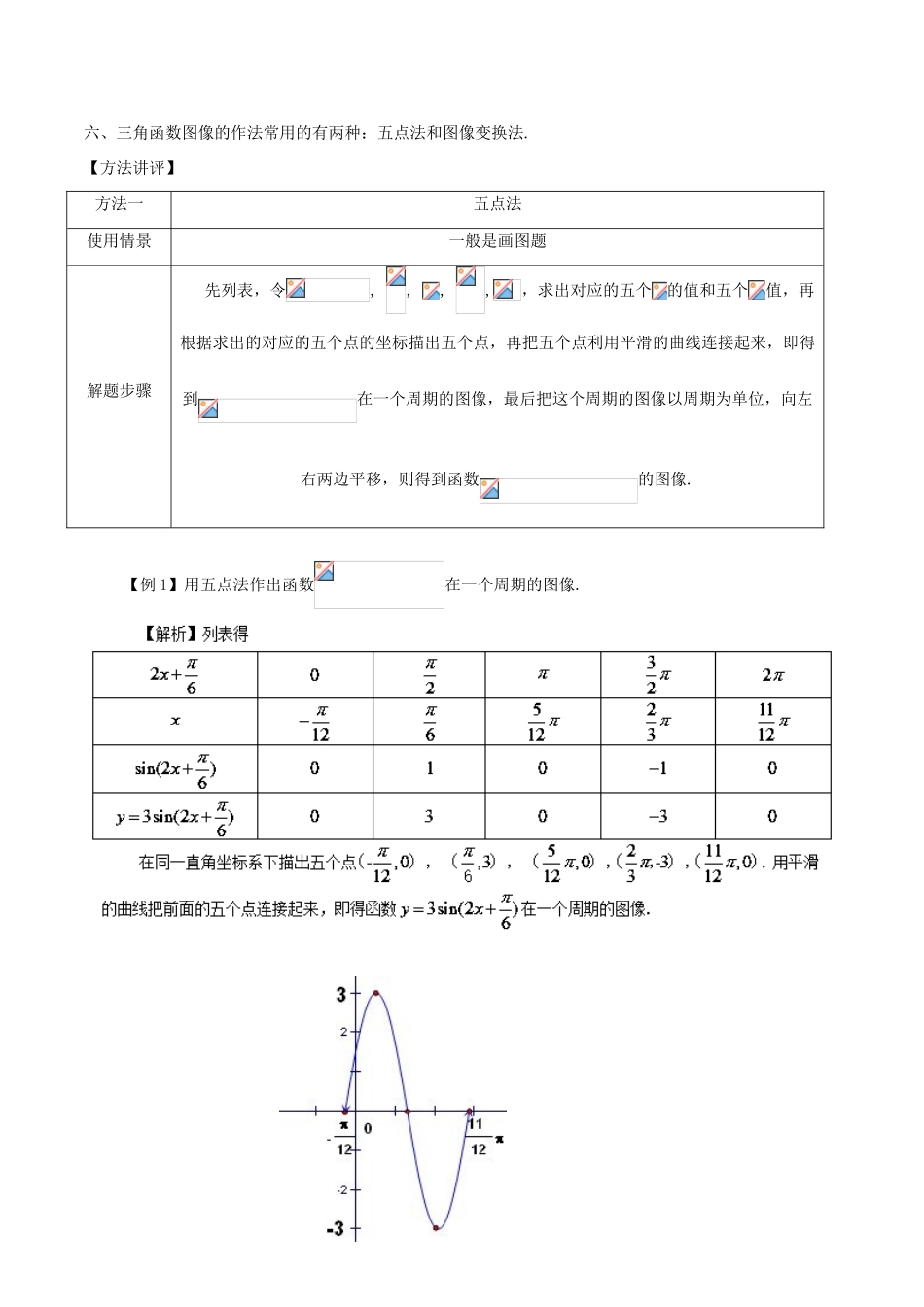
第27讲三角函数图象的作法【知识要点】一、三角函数的图像二、(或)图象的作法有两种:(1)描点法(五点法),先列表,令,,,,,求出对应的五个的值和五个值,再根据求出的对应的五个点的坐标描出五个点,再把五个点利用平滑的曲线连接起来,即得到在一个周期的图像,最后把这个周期的图像以周期为单位,向左右两边平移,则得到函数的图像.(2)图像变换法:一般先把函数的图像通过左右平移得到函数的图像,再把xy0xy0函数的图像通过横坐标的伸缩变换得到函数,再把函数通过纵坐标的伸缩变换得到函数的图像,最后把函数的图像通过上下平移得到函数的图像.三、三角函数图像的变换(平移变换和上下变换)平移变换:左加右减,上加下减把函数向左平移个单位,得到函数的图像把函数向右平移个单位,得到函数的图像把函数向上平移个单位,得到函数的图像把函数向下平移个单位,得到函数的图像伸缩变换:①把函数图象的纵坐标不变,横坐标伸长到原来的倍得②把函数图象的纵坐标不变,横坐标缩短到原来的倍得③把函数图象的横坐标不变,纵坐标伸长到原来的倍得④把函数图象的横坐标不变,纵坐标缩短到原来的倍得四、用“五点法”作正余弦函数的图象要注意必须先将解析式化为或的形式.五、三角函数图像的变换的方式并不是唯一的,可以有多种变换方式.可以先左右平移,再伸缩,后上下.也可以先伸缩,再左右平移,后上下.但是三角函数图像的变换一般先选择左右平移,再进行其它变换.这样容易理解,计算也简单.六、三角函数图像的作法常用的有两种:五点法和图像变换法.【方法讲评】方法一五点法使用情景一般是画图题解题步骤先列表,令,,,,,求出对应的五个的值和五个值,再根据求出的对应的五个点的坐标描出五个点,再把五个点利用平滑的曲线连接起来,即得到在一个周期的图像,最后把这个周期的图像以周期为单位,向左右两边平移,则得到函数的图像.【例1】用五点法作出函数在一个周期的图像.【点评】(1)对于我们常见的初等函数(一次函数、正比例函数、反比例函数、二次函数、对数函数、指数函数、三角函数等),由于我们知道函数的图像和性质,所以我们常用描点法直接作函数的图像.(2)利用五点法作的图像,列表时,第一行不是的值,是的值,描点时,是以描点,这一点要注意.【反馈检测1】设函数.(1)在给出的直角坐标系中画出函数在区间上的图象;(2)根据画出的图象写出函数在上的单调区间和最值.方法二图像变换法使用情景一般不是画图题.解题步骤一般先把函数的图像通过左右平移得到函数的图像,再把函数的图像通过横坐标的伸缩变换得到函数,再把函数通过纵坐标的伸缩变换得到函数的图像,最后把函数的图像通过上下平移得到函数的图像.【例2】已知函数,.(I)求函数的单调增区间;(Ⅱ)函数的图象可以由函数()的图象经过怎样的变换得到?(II)方法一:先把图象上所有点向左平移个单位长度,得到的图象,再把所得图象上所有的点向上平移个单位长度,就得到的图象.方法二:先把图象上所有点向上平移个单位长度得到函数的图像,再把函数的图像向左平移个单位长度得到的图象.【点评】(1)三角函数图像的变换的方式并不是唯一的,可以有多种变换方式.可以先左右平移,再伸缩,后上下.也可以先伸缩,再左右平移,后上下.(2)三角函数图像的变换一般先选择左右平移,再进行其它变换.如:由函数得到函数的图像,一般先把函数的图像向左平移个单位得到函数的图像,再把函数的图像的横坐标伸长到原来的2倍得到函数的图像.也可以这样,先把函数的图像的横坐标伸长到原来的2倍得到函数的图像,再把函数的图像向左平移个单位得到函数.显然后面的一种不容易理解,并且要计算,不像第一种容易理解,且不需要计算,所以对于三角函数一般先左右,再进行其它变换.【例3】怎样将函数的图像变换得到函数的图像?【解析】方法一:(逆向思维)一般情况下,我们是把一个简单的函数通过图像变换得到复杂函数的图像,但是此题是把复杂的函数通过图像变换得到简单的函数的图像,所以我们可以先考虑由函数的图像得到函数的图像,因为,所以要把函数的图像向右平移个单位.所以将函数的图像向左平移...