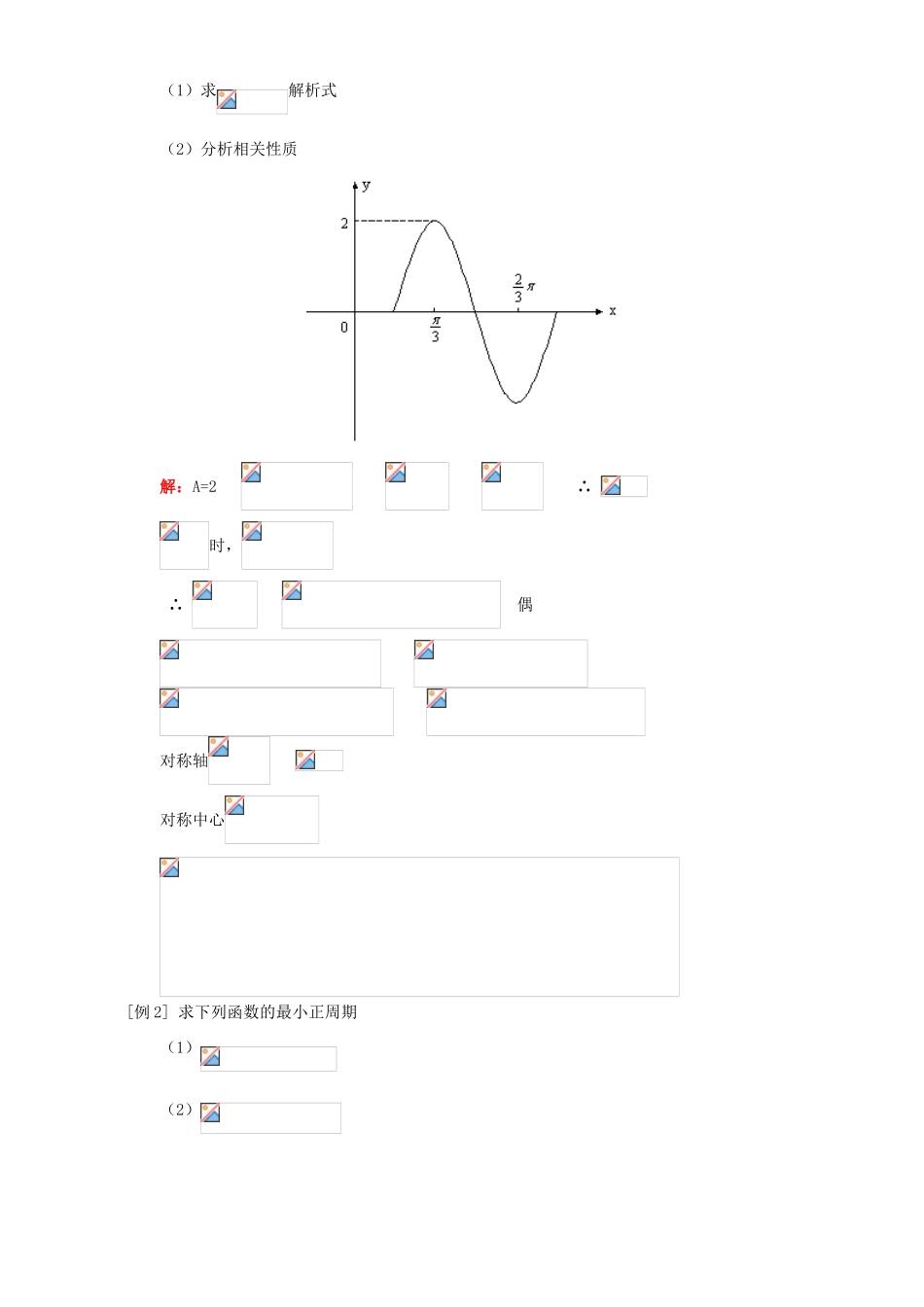
函数的图象性质例题解析一.本周教学内容:的图象性质二.重点、难点:1.定义域:R值域:奇偶性:单调性:最小正周期:对称轴:对称中心:振幅:A频率:相位:初相:2.若,则利用调整为正3.若,则利用调整为正【典型例题】[例1]的一个周期的图象如图,,(1)求解析式(2)分析相关性质解:A=2∴时,∴偶对称轴对称中心[例2]求下列函数的最小正周期(1)(2)(3)解:(1)(2)(3)如图(略)[例3]求下列函数增区间(1)(2)(3)(4)(5)(6)解:(1)(2)(3)(4)∴(5)(6)分析图象[例4]已知,求的最值。解:令代入∴时,时,[例5]平移,填空(1)的图象,纵坐标不变横坐标再向得的图象。(2)的图象,纵坐标不变,向再将横坐标得的图象。(3)的图象,(经两步)得图象。(4)的图象,(经两步),得的图象。解:(1)缩为原长的,向右平移(2)向右平移,缩为原长(3);横向左,缩为(4)横坐标,向左,缩为[例6]函数(,)在其一个周期图象上有一个最高点()和一个最低点()求这个函数解析式。解:∴时,∴[例7]已知某海滨浴场的海浪高度y(米)是时间t(小时的函数,记作,下表为某日各时的浪高数据)036912151821241.51.00.51.01.510.50.991.5经过长期观察的曲线可近似看成函数(1)求解析式(2)浪高1m以上最适合冲浪每日从早上8:00至晚上20:00中适合冲浪的时间为几小时。解:由表格,∴A=∴∴∴又∵∴为6小时[例8]已知,求的取值范围。解:∴∵∴∴[例9],若,则有可能的值为()A.1B.C.D.解:∴(1)(2)∴∴C1.以下四个函数有()个周期函数。①②③④A.1B.2C.3D.42.函数的最小值为()A.B.C.D.03.函数的最小正周期为()A.B.C.D.4.下列函数最小正周期为的是()A.B.C.D.5.为R上的奇函数,,时,,则()A.B.C.D.6.已知,要使成立,只需()A.B.C.D.[参考答案]1.A2.B3.B4.B5.B6.B