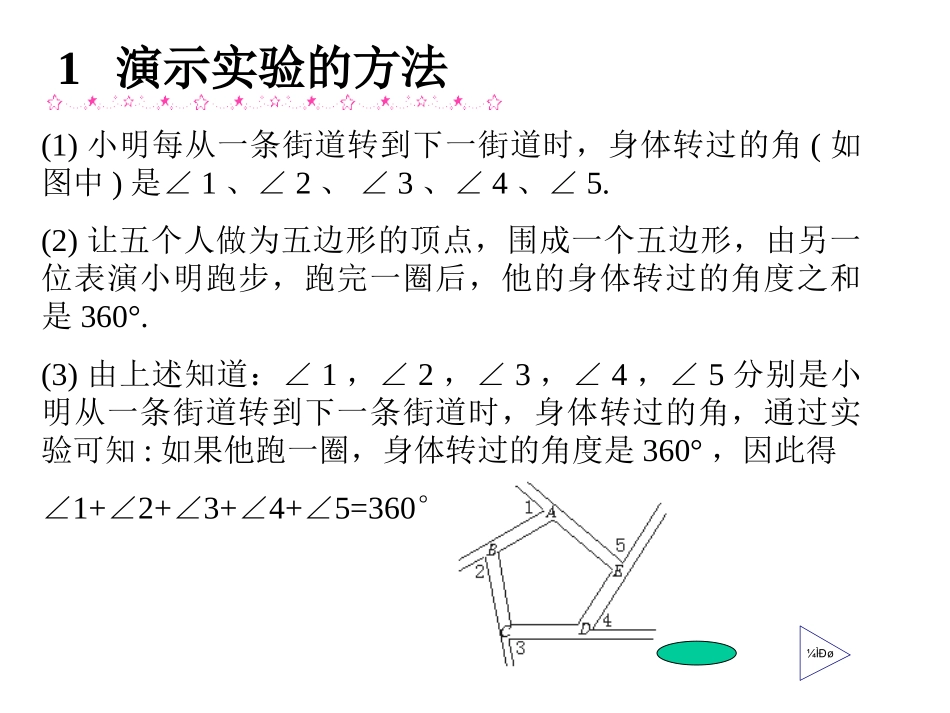
一问题的指出大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图.请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.(2)他每跑完一圈,身体转过的角度之和是多少?(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?1演示实验的方法(1)小明每从一条街道转到下一街道时,身体转过的角(如图中)是∠1、∠2、∠3、∠4、∠5.(2)让五个人做为五边形的顶点,围成一个五边形,由另一位表演小明跑步,跑完一圈后,他的身体转过的角度之和是360°.(3)由上述知道:∠1,∠2,∠3,∠4,∠5分别是小明从一条街道转到下一条街道时,身体转过的角,通过实验可知:如果他跑一圈,身体转过的角度是360°,因此得∠1+∠2+∠3+∠4+∠5=360°.¼ÌÐø如图所示,过平面内一点O分别作与五边形ABCDE各边平行的射线OA′、OB′、OC′、OD′、OE′,得到∠α、∠β、∠γ、∠δ、∠θ,其中:∠α=∠1,∠β=∠2,γ∠=∠3,δ∠=∠4,θ∠=∠5.而通过测量知:∠α、∠β、∠γ、∠δ、∠θ恰好组成一个周角.这样,∠1、∠2、∠3、∠4、∠5的和等于360°.2实验与测量相结合的方法¼ÌÐø10987654321解:∵∠1+6=180°∠,∠2+7=180°∠,∠3+8=180°∠,∠4+9=180°∠,∠5+10=180°∠∴∠1+2+3+4+5+6+7+8+9+10=900°∠∠∠∠∠∠∠∠∠而∠1+2+3+4+5=540°∠∠∠∠∴∠6+∠7+∠8+∠9+∠10=360°3推理证明法:¼ÌÐø多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角(exteriorangle)在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.一般地,在多边形的任一顶点处按顺(逆)时针方向可作外角,n边形有n个外角.54321二新课:三探索:分别求出下列多边形的外角和的度数.32143215432165432187654321360°360°360°360°360°四猜想与说理:n边形的外角和是多少度呢?答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°=360°.定理:多边形的外角和都等于360°.[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形?解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形.五例题赏析六课堂练习:1.一个多边形的外角都等于60°,这个多边形是n边形?解:因为多边形的外角和等于360°,所以根据题意,可知道这个多边形的边数是:360÷60=6.答:这个多边形是六边形.2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么?解:设:这个正多边形的一个内角为x°,则由题图得:3x=360°.x=120°.再根据多边形的内角和公式得:n×120°=(n-2)×180°.解得n=6.答:(略)1.是否存在一个多边形,它的每个内角都等于相邻外角的五分之一?为什么?解:不存在,理由是:如果存在这样的多边形,设它的一个外角为α,则对应的内角为180°-α,于是:α=5×(180°-α),解得α=150°.而多边形的外角和为360°,可得这个多边形的边数为:360°÷150°=2.4,而边数应是整数,因此不存在这样的多边形.七试一试2.在四边形的四个内角中,最多能有几个钝角?最多能有几个锐角?解:最多能有三个钝角,最多能有三个锐角.理由是:设四边形的四个内角的度数分别为:α°,β°,γ°,δ°,则α+β+γ+δ=360°,α、β、γ、δ的值最多能有三个大于90°,否则α、β、γ、δ都大于90°.α+β+γ+δ>360°.同理最多能有三个角小于90°.八课时小结:多边形的外角和与多边形的边数无关,它恒等于360°.九、课后作业(一)课本P112习题4.121、2、3(二)1.预习内容:P113