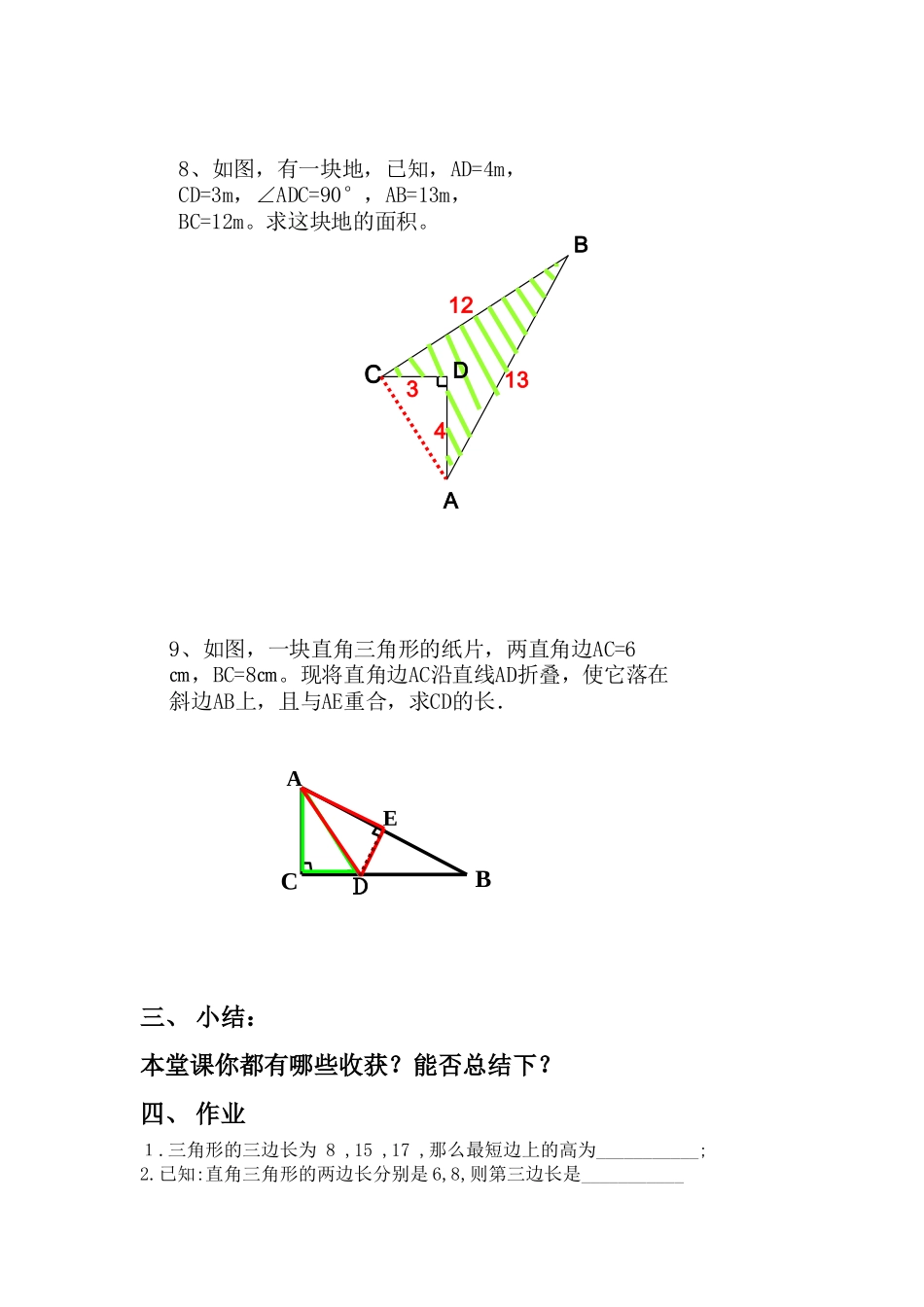
复习:勾股定理及其逆定理教学目标:1.回顾熟知勾股定理,勾股定理逆定理,理解它们的产生及证明过程,形成体系,能运用勾股定理及逆定理进行计算、证明和解决实际问题.2.理解互逆命题、互逆定理、勾股数的概念,能写出一个命题的逆命题.重难点:勾股定理及逆定理的应用.教学过程:一、知识点回顾:a2+b2=c2形数a2+b2=c2三边a、b、cRt△直角边a、b,斜边cRt△互逆命题勾股定理:直角三角形的两直角边为a,b,斜边为c,则有三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形;较大边c所对的角是直角.逆定理:a2+b2=c2互逆命题:两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个叫做另一个的逆定理.命题:1、对顶角相等的逆命题是2、等腰三角形两底角相等的逆命题:二、练习巩固:1、在直角三角形ABC中,∠C=90°,(1)已知a:b=3:4,c=20,求a和b(2)已知∠A=30°a=3,求b和c(3)已知∠A=45°,c=8,求a和b2、直角△的两边长为3和4,求第三边的长度.3、已知等边三角形的边长为2厘米,则它的高为_____,面积为_____.4、判断以线段a、b、c为边的△ABC是不是直角△(1)a=3,b=6,c=9(2)a=6,b=10,c=85.已知三角形的三边长为9,12,15,则这个三角形的最大角是____度;6.△ABC的三边长为9,40,41,则△ABC的面积为____;7.如图,两个正方形的面积分别为64,49,则AC=.ADC64498、如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。ABC341312D9、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.ACDBE第8题图D三、小结:本堂课你都有哪些收获?能否总结下?四、作业1.三角形的三边长为8,15,17,那么最短边上的高为___________;2.已知:直角三角形的两边长分别是6,8,则第三边长是___________3.若△ABC中,AB=5,BC=12,AC=13,则AC边上的高长为_________;4、在△ABC中,∠C=90°,AC=3,CB=4.(1)求△ABC的面积(2)求斜边AB(3)求高CDCABD5、已知,如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=1.5,BD=2.5,求AC的长.DACB12