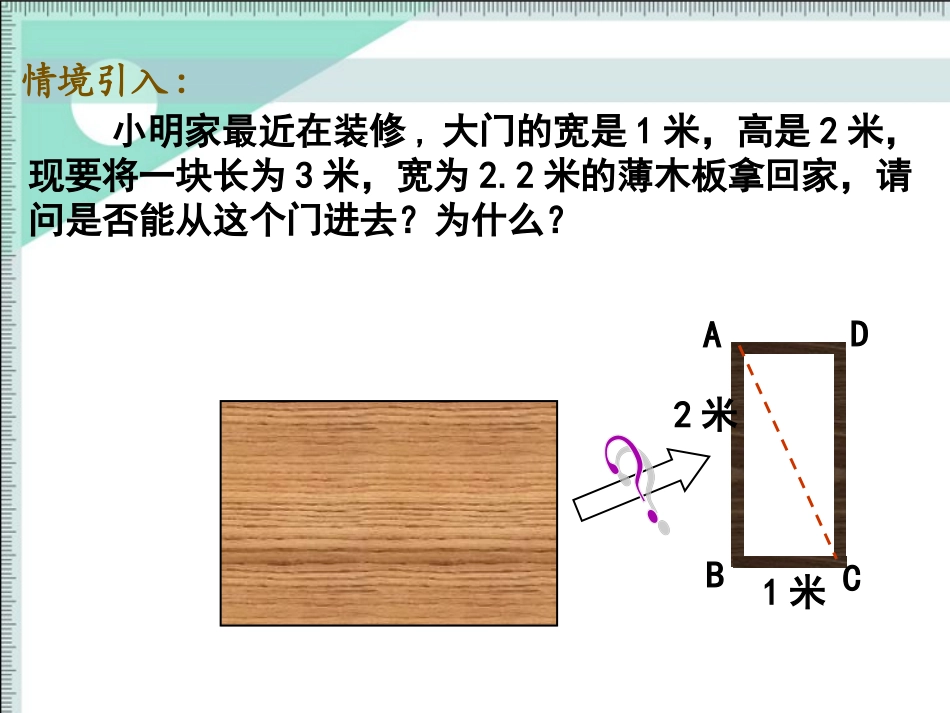
执教者:李素怀执教者:李素怀情境引入:小明家最近在装修,大门的宽是1米,高是2米,现要将一块长为3米,宽为2.2米的薄木板拿回家,请问是否能从这个门进去?为什么?DCAB2米1米问题:P、Q、R的面积有何数量关系?问题:Rt△ABC三边有什么数量关系?观察:CBA相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么?SP+SQ=SRBC2+AC2=AB2PQR等腰直角三角形两直角边的平方和等于斜边的平方。思考:等腰直角三角形三边之间有此关系,其他的直角三角形有这种关系吗?PQRPQRP的面积(单位长度)Q的面积(单位长度)R的面积(单位长度)图2图3P、Q、R面积关系直角三角形三边关系图2图3491392534SP+SQ=SR两直角边的平方和等于斜边的平方探究:在Rt△ABC中,直角边AC、BC与斜边AB有怎样的等量关系?ABCABC即:BC2+AC2=AB2命题:如果直角三角形两直角边分别为a,b,斜边为c,那么;a2+b2=c2cab猜想:bca大正方形的面积该怎样表示?探究:证明一:ccccba(a-b)2这四个直角三角形还能怎样拼?baCccc证明二:大正方形的面积该怎样表示?探究:cabbbbaaac在Rt△ABC中,直角边AC、BC的平方和等于斜边AB的平方。即AC2+BC2=AB2或b2+a2=c2。aBACbcaab.b赵爽的证法证明三:探究:ABCDEFGMc在Rt△ABC中,直角边AC、BC的平方和等于斜边AB的平方。即AC2+BC2=AB2或b2+a2=c2。aBACbcaab.b赵爽的证法证明三:探究:ABCDEFGM我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦。弦股勾如右下图称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。它被选为2002年在北京召开的国际数学家大会的会徽。赵爽弦图阅读:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2cab定理:命题:即:直角三角形两直角边的平方和等于斜边的平方.探究:直角三角形c2=a2+b222baca2=c2-b222bcab2=c2-a222acb(毕达哥拉斯定理)小明家最近在装修,大门的宽是1米,高是2米,现要将一块长为3米,宽为2.2米的薄木板拿回家,请问是否能从这个门进去?为什么?已知,在Rt△ABC中,∠B=900,BC=1,AB=2,问AC与2.2的大小?解:∵在Rt△ABC中,∠B=9005答:薄木板能从这个门进去。∴AC2=BC2+AB2=12+22=5∴AC=≈2.236>2.2例题:DCAB2米1米45(1)1、请直接算出下列各直角三角形中未知边的长;练习:x610(3)125(2)2、一只蚂蚁沿图中的折线从A点爬到D,一共爬了多少厘米?(小方格的边长为1厘米)3x8x13BCEGFAD43512513681024m5、如图,因台风,一根高24米的木制电线杆在离地面9米处出现了裂痕,随时都可能倒下,十分危急。接警后“110”迅速赶到现场,并决定从断裂处将电线杆折断,现在需要划出一个安全警戒区域,请你确定这个警戒区域的半径?拓展:9mCBDA变形2:电线杆高24米,在某处断裂后倒下,电线杆顶部落在离底部12米处,求电线杆在离地面多少米处断裂?12m300变形1:电线杆高24米,在某处断裂后倒下,电线杆顶部落地后,与地面成300角,求电线杆在离地面多少米处断裂?1、这节课我的收获是——;2、我最感兴趣的地方是—;3、我想进一步研究的问题是———。收获与体会收获与体会1.课本第80页,习题1-2。2.查阅勾股定理的历史及勾股定理的证明。3.实践活动:收集生活中利用勾股定理解决的实际问题,互相交流。作业设计作业设计作业设计作业设计勾股定勾股定理理猜想猜想应用应用拓展拓展体会体会证明证明观察观察