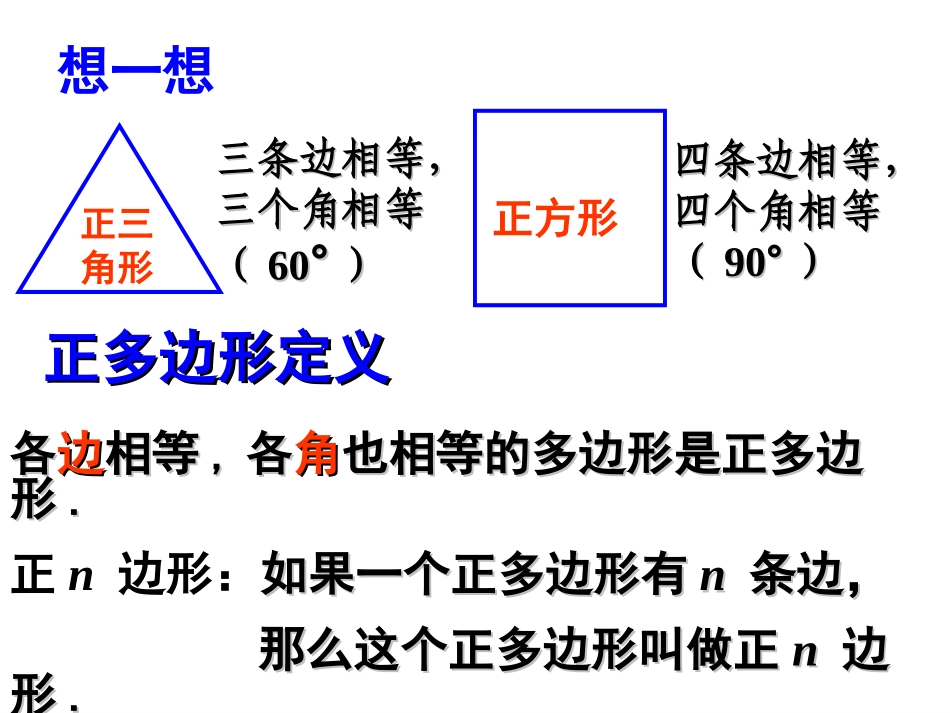
第二十四章圆第第11课时课时24.324.3正多边形和圆正多边形和圆观察下列图形,从这些图形中找出相应的正多边形.各各边边相等相等,,各各角角也相等的多边形是正多边也相等的多边形是正多边形形..正n边形:如果一个正多边形有如果一个正多边形有nn条边,条边,那么这个正多边形叫做正那么这个正多边形叫做正nn边边形形..三条边相等,三条边相等,三个角相等三个角相等((6060°°))四条边相等,四条边相等,四个角相等四个角相等((9090°°))正三角形正方形正多边形定义正多边形定义想一想你知道正多边形与圆的关系吗?正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.探索新知·ABCDEOABCDE如图,把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴AB=BC=CD=DE=EA,∴∠A=∠B.·ABCDEO同理∠B=∠C=∠D=∠E.又∵五边形ABCDE的顶点都在⊙O上,∴五边形ABCDE是⊙O的内接正五边形,⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.∵AB=BC=CD=DE=EA∴BCE=CDA=3AB③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB)①我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心(即点O)②外接圆的半径叫做正多边形的半径(即OA)④中心到正多边形的一边的距离叫做正多边形的边心距(即OM)引入新知O·中心角半径R边心距rABCDEFM正多边形的外接圆圆内接正多边形ABCDEFOO圆心角中心角ABCDEFCDABMM半径R半径R圆心中心弦心距r边心距r弦边外接圆⊙O圆内接正多边形圆心O中心O半径OA(R)半径OA(R)圆心角∠AOB中心角∠AOB弦心距OM(r)边心距OM(r)弦CD边CDABEF.CCDDOOMM连接OC,由垂径定理(运用圆的有关知识)得CDCM21nnCOM1803602121中心角.RtΔ222CMOMOCCOM中,有在中心角一半边长一半半径R边心距rMCO603180336021213中心角时,当COMn454180436021214中心角时,当COMn306180636021216中心角时,当COMn边心距r半径R60OMC边心距r半径R45OMC边心距r半径R30MCO)边心距()边心距(面积,边心距)(rnarLSraR2121222EFCD...OO中心角中心角n360中心角nBOGAOG180AABBGG边心距OG把△AOB分成2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例.有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解:如图由于ABCDEF是正六边形,所以它的中心角等于,△OBC是等边三角形,从而正六边形的边长等于它的半径.因此,亭子地基的周长l=4×6=24(m).OABCDEFRPr360606例题讲解利用勾股定理,可得边心距224223.r亭子地基的面积211242341.6(m).22Slr在Rt△OPC中,OC=4,PC=4222BC,例题讲解OABCDEFRPr巩固练习1.正八边形的每个内角是______度.135°2.如图,正六边形ABCDEF内接于⊙O,则∠CFD的度数是()A.60°B.45°C.30°D.22.5°C3.如果一个正多边形绕它的中心旋转90°就与原来的图形重合,那么这个正多边形是()A.正三角形B.正方形C.正五边形D.正六边形B4.已知正六边形的边心距为,则它的周长是_____.3125.如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.OFEDCBAxyA(-1,)3B(-2,0)C(-1,)3D(1,)3E(2,0)F(1,)36.如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为()A.40B.50C.60D.80BACDEFGHA7.边长为6的正三角形的半径是________.32ABCDEFO8.如图,⊙O的周长为cm,求以它的半径为边长的正六边形ABCDEF的面积.π62cm2327S课堂小结这节课中,你有哪些收获?解决问题的方法是什么?还有哪些疑惑?课后作业:教科书第107---108页1,3,5,6题.