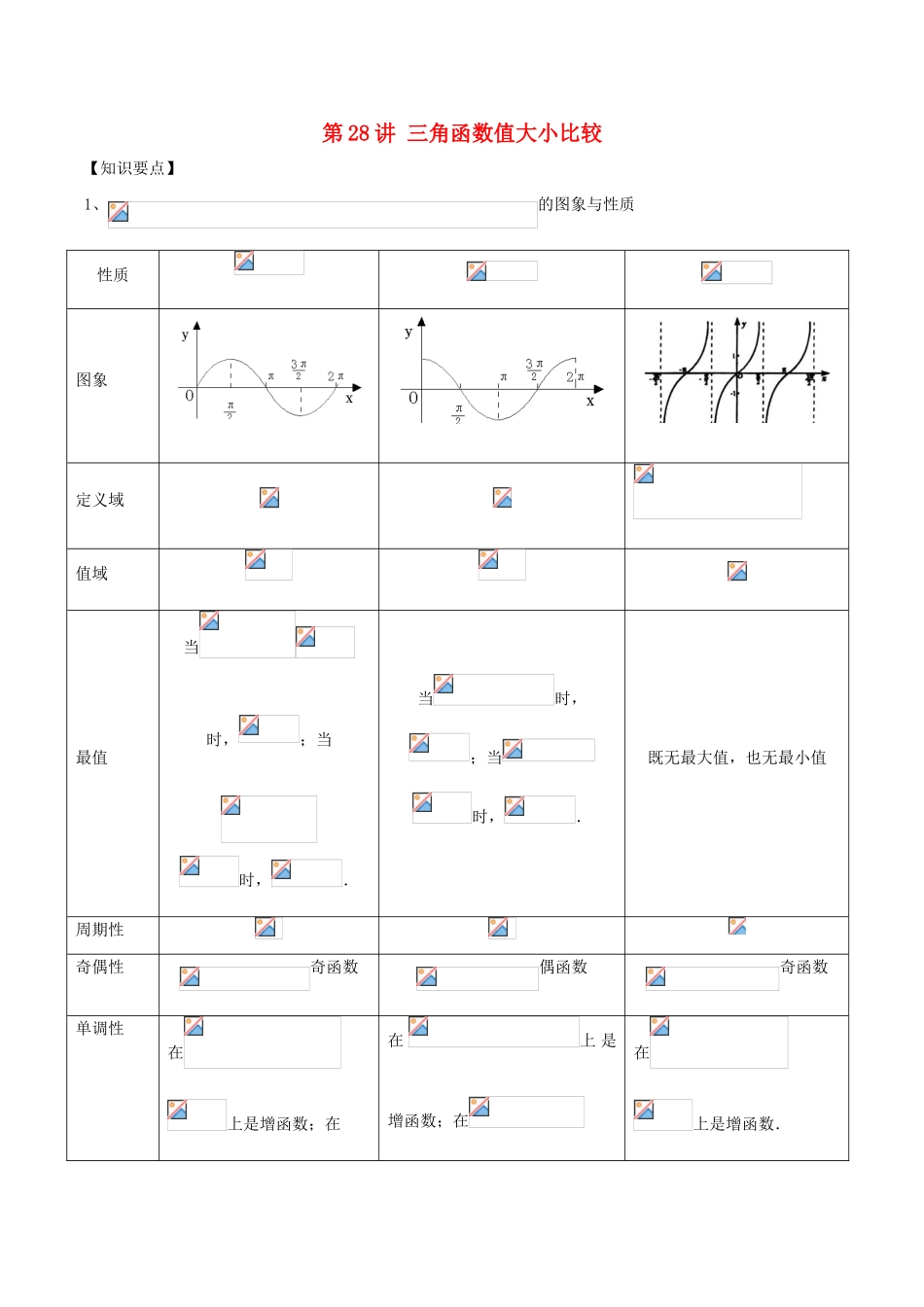
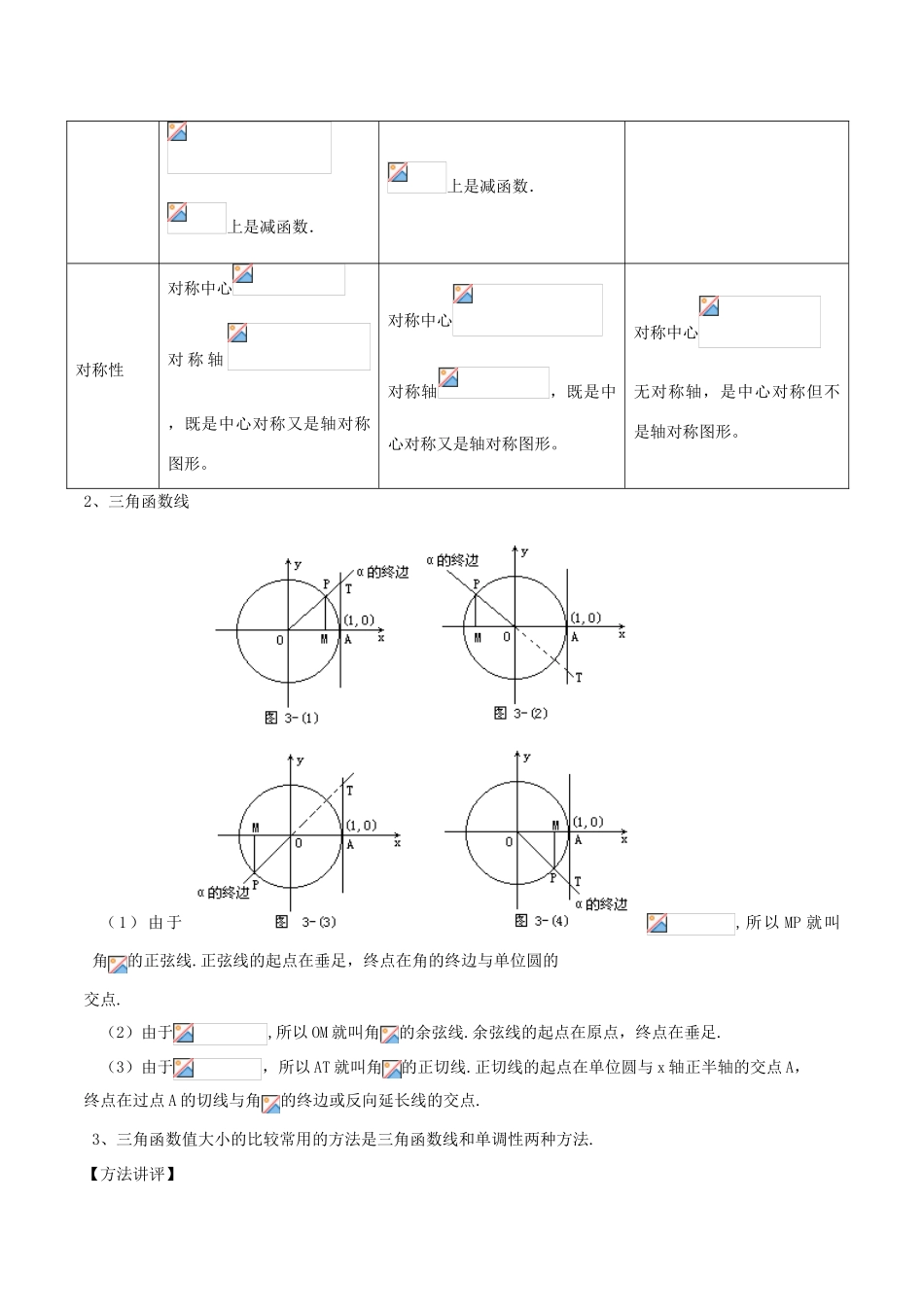
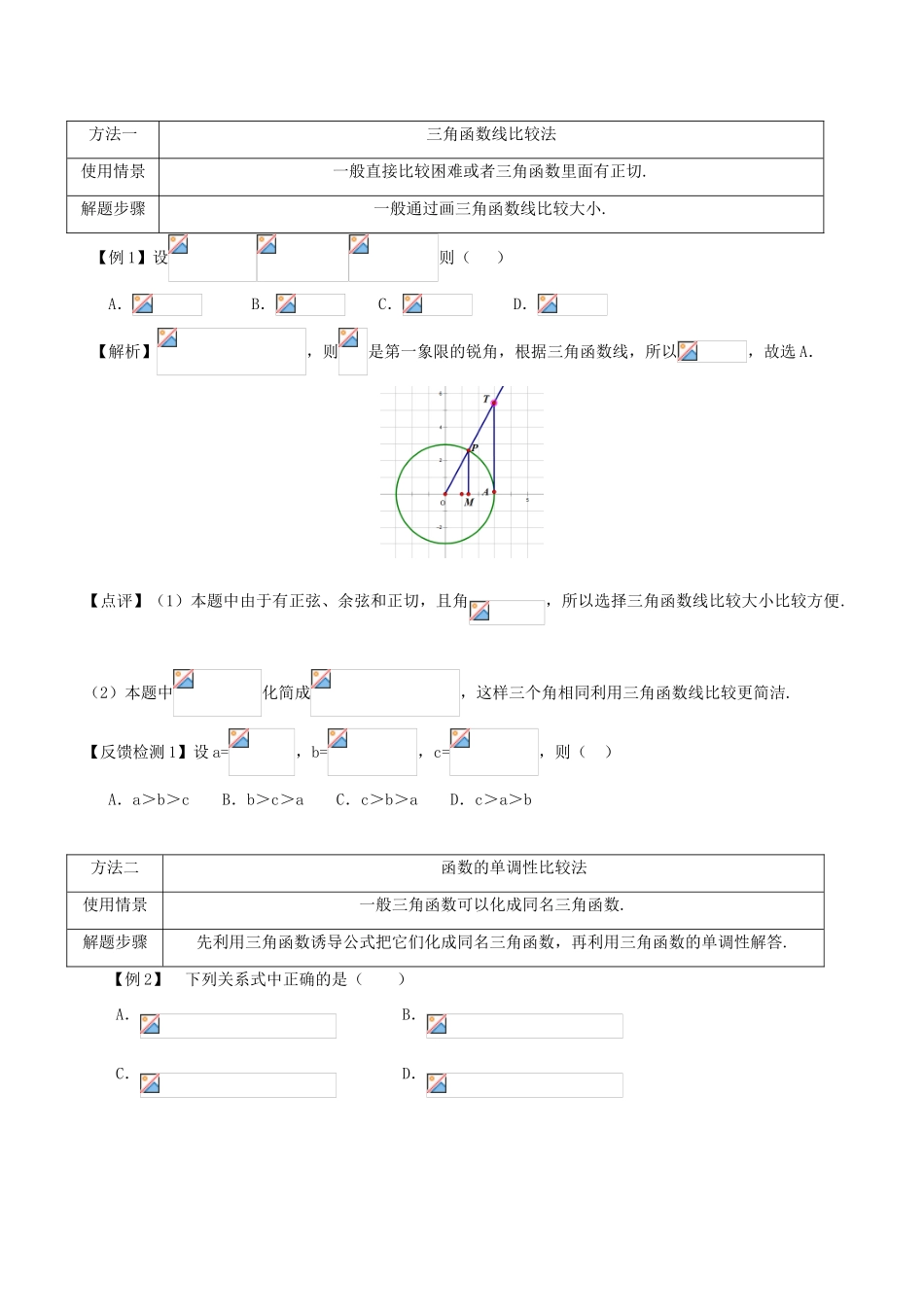
第28讲三角函数值大小比较【知识要点】1、的图象与性质性质图象定义域值域最值当时,;当时,.当时,;当时,.既无最大值,也无最小值周期性奇偶性奇函数偶函数奇函数单调性在上是增函数;在在上是增函数;在在上是增函数.上是减函数.上是减函数.对称性对称中心对称轴,既是中心对称又是轴对称图形。对称中心对称轴,既是中心对称又是轴对称图形。对称中心无对称轴,是中心对称但不是轴对称图形。2、三角函数线(1)由于,所以MP就叫角的正弦线.正弦线的起点在垂足,终点在角的终边与单位圆的交点.(2)由于,所以OM就叫角的余弦线.余弦线的起点在原点,终点在垂足.(3)由于,所以AT就叫角的正切线.正切线的起点在单位圆与x轴正半轴的交点A,终点在过点A的切线与角的终边或反向延长线的交点.3、三角函数值大小的比较常用的方法是三角函数线和单调性两种方法.【方法讲评】方法一三角函数线比较法使用情景一般直接比较困难或者三角函数里面有正切.解题步骤一般通过画三角函数线比较大小.【例1】设则()A.B.C.D.【解析】,则是第一象限的锐角,根据三角函数线,所以,故选A.【点评】(1)本题中由于有正弦、余弦和正切,且角,所以选择三角函数线比较大小比较方便.(2)本题中化简成,这样三个角相同利用三角函数线比较更简洁.【反馈检测1】设a=,b=,c=,则()A.a>b>cB.b>c>aC.c>b>aD.c>a>b方法二函数的单调性比较法使用情景一般三角函数可以化成同名三角函数.解题步骤先利用三角函数诱导公式把它们化成同名三角函数,再利用三角函数的单调性解答.【例2】下列关系式中正确的是()A.B.C.D.【点评】由于要比较的对象只有正弦和余弦,所以可以通过诱导公式把它们统一化成正弦,再利用正弦函数的单调性解答.【反馈检测2】下列不等式中,正确的是()A.B.C.D.高中数学常见题型解法归纳及反馈检测第28讲:三角函数值大小比较参考答案【反馈检测1答案】C【反馈检测2答案】B【反馈检测2详细解析】函数在区间为单调递增函数,在区间为单调递增函数,由,由,故A,C错误;在区间为单调递增函数,,由,即,故B正确;,所以有,故D错误,综上所述,选B.