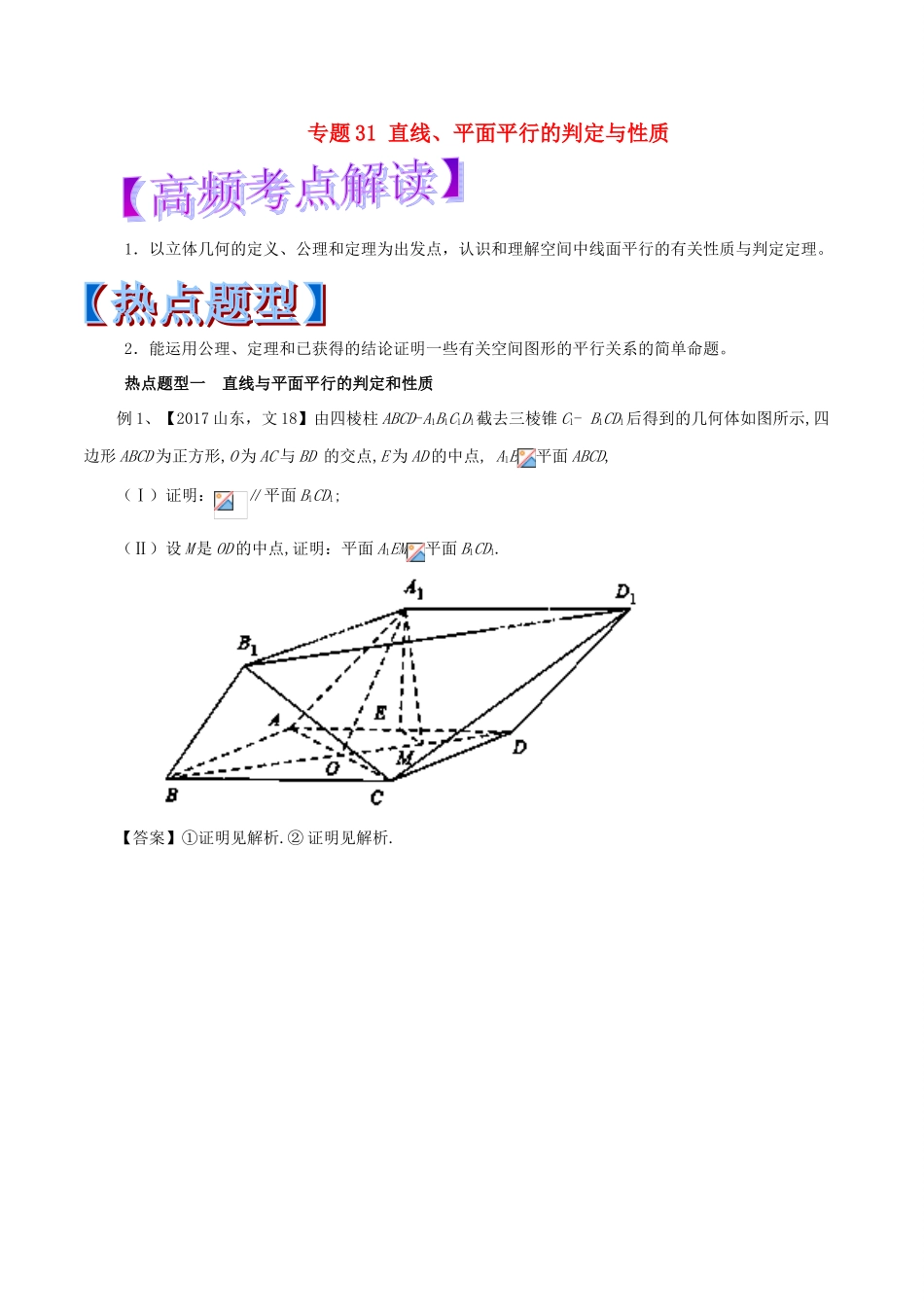
专题31直线、平面平行的判定与性质1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定定理。2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题。热点题型一直线与平面平行的判定和性质例1、【2017山东,文18】由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E平面ABCD,(Ⅰ)证明:∥平面B1CD1;(Ⅱ)设M是OD的中点,证明:平面A1EM平面B1CD1.【答案】①证明见解析.②证明见解析.【变式探究】如图所示,已知P、Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心。证明:PQ∥平面BCC1B1。证明:方法一,如图①,取B1B中点E,BC中点F,连接PE、QF、EF,①【提分秘籍】证明线面平行的关键点及探求线线平行的方法(1)证明直线与平面平行的关键是设法在平面内找到一条与已知直线平行的直线;(2)利用几何体的特征,合理利用中位线定理、线面平行的性质,或者构造平行四边形、寻找比例式证明两直线平行;(3)注意说明已知的直线不在平面内,即三个条件缺一不可。【举一反三】如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD,且AB⊥CD,试问截面在什么位置时其截面面积最大?热点题型二平面与平面平行的判定和性质例2、如图所示,三棱柱ABC-A1B1C1中,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,求证:平面A1BD1∥平面AC1D。【提分秘籍】平面平行的判定定理,是利用了线面平行来推证的,即需要找到或证出两条相交直线平行另一平面。本题的证明就是运用了这一判定定理。【举一反三】如图所示,平面α∥平面β,A、C∈α,B、D∈β,点E、F分别在线段AB、CD上,且=,求证:EF∥平面β。【解析】当AB和CD在同一平面内时,由α∥β可知AC∥BD,ABDC是梯形或平行四边形。由=,得EF∥BD。热点题型三平行关系中的探索性问题例3.如图所示,斜三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的点。(1)当等于何值时,BC1∥平面AB1D1?(2)若平面BC1D∥平面AB1D1,求的值。所以当=1时,BC1∥平面AB1D1。(2)由平面BC1D∥平面AB1D1,且平面A1BC1∩平面BC1D=BC1,平面A1BC1∩平面AB1D1=D1O得BC1∥D1O,所以=,又由题可知=,=1,所以=1,即=1。【提分秘籍】与平行有关的探索性问题求解策略平行关系中的探索性问题,一般是先根据条件猜测点的位置再进行证明,多为中点或三等分点问题。【举一反三】如图,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内有BE⊥PC于E,且BE=a,试在AB上找一点F,使EF∥平面PAD。【解析】在平面PCD内,过E作EG∥CD交PD于G,连接AG,在AB上取点F,使AF=EG,则F即为所求作的点。∴CP==a。又 ==,∴EG=AF=a。∴点F为AB的一个三等分点。1.【2017山东,文18】(本小题满分12分)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E平面ABCD,(Ⅰ)证明:∥平面B1CD1;(Ⅱ)设M是OD的中点,证明:平面A1EM平面B1CD1.【答案】①证明见解析.②证明见解析.【解析】证明:1.【2016高考山东文数】(本小题满分12分)在如图所示的几何体中,D是AC的中点,EF∥DB.(I)已知AB=BC,AE=EC.求证:AC⊥FB;(II)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.【答案】(Ⅰ))证明:见解析;(Ⅱ)见解析.【解析】(Ⅰ)证明:因,所以与确定平面.2.【2016高考天津文数】(本小题满分13分)如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=,DE=3,∠BAD=60º,G为BC的中点.(Ⅰ)求证:平面BED;(Ⅱ)求证:平面BED⊥平面AED;(Ⅲ)求直线EF与平面BED所成角的正弦值.【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)【解析】(Ⅰ)证明:取中点,连接,在中,因为是中点,所以且,又因为,所以且,即四边形是平行四边形,所以,又平面,平面,所以平面.(Ⅱ)证明:在中,°,由余弦定理可得,进而得1.【2015高考浙江,文4】设,是两个不同的平面,,是两条不同的直线,且,()A.若,则B.若,则C.若,则D.若,则【答案...