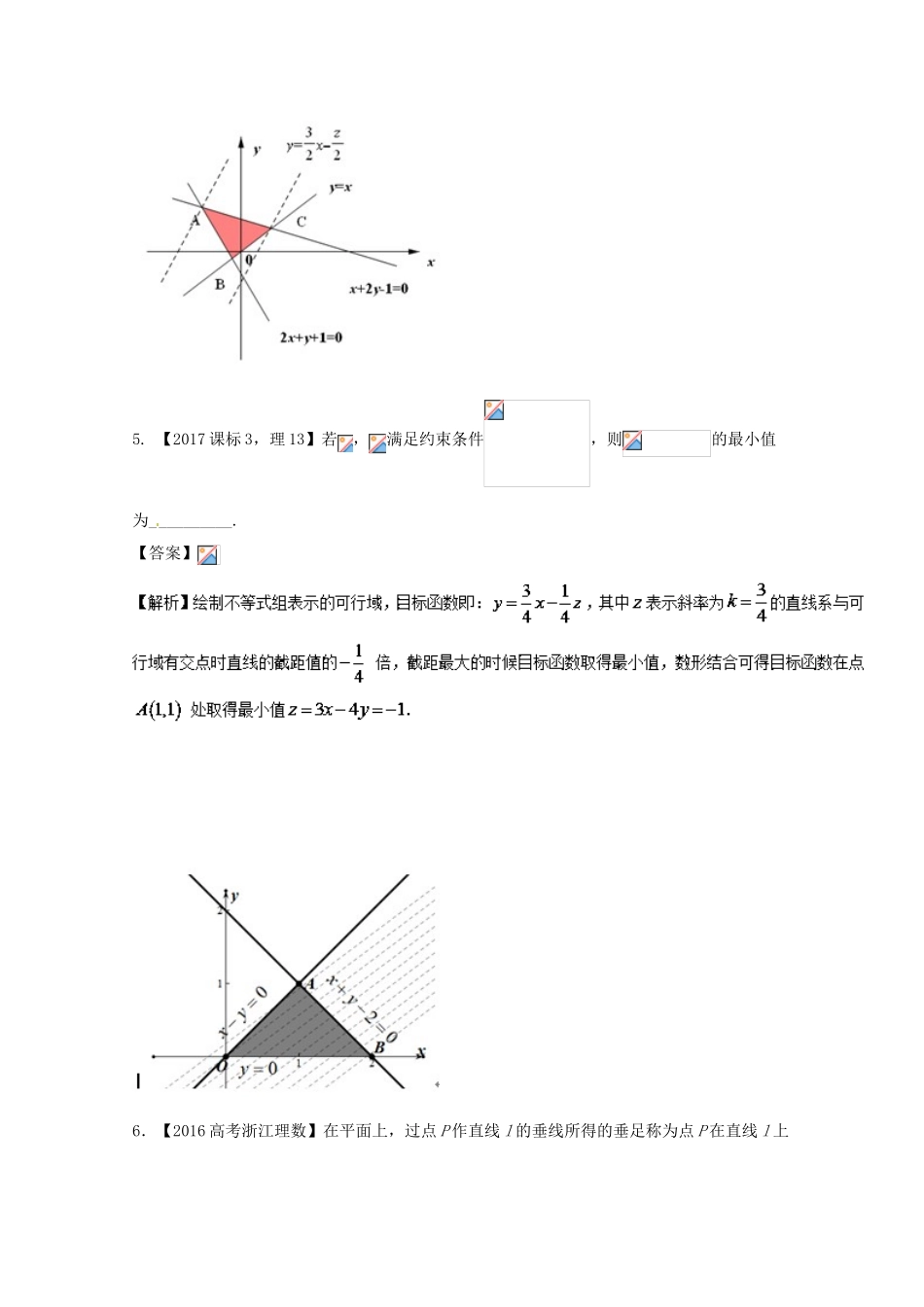
专题7.2二元一次不等式(组)与简单的线性规划问题【三年高考】1.【2017课标II,理5】设,满足约束条件,则的最小值是()A.B.C.D.【答案】A【解析】绘制不等式组表示的可行域,目标函数即:,其中表示斜率为的直线系与可行域有交点时直线的截距值,数形结合可得目标函数在点处取得最小值,故选A。2.【2017天津,理2】设变量满足约束条件则目标函数的最大值为(A)(B)1(C)(D)3【答案】【解析】目标函数为四边形ABCD及其内部,其中,所以直线过点B时取最大值3,选D.3.【2017浙江,4】若,满足约束条件,则的取值范围是A.[0,6]B.[0,4]C.[6,D.[4,【答案】D【解析】如图,可行域为一开放区域,所以直线过点时取最小值4,无最大值,选D.4.【2017课标1,理13】设x,y满足约束条件,则的最小值为.【答案】【解析】不等式组表示的可行域如图所示,易求得,由得在轴上的截距越大,就越小所以,当直线直线过点时,取得最小值所以取得最小值为.5.【2017课标3,理13】若,满足约束条件,则的最小值为__________.【答案】6.【2016高考浙江理数】在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x+y2=0上的投影构成的线段记为AB,则│AB│=()A.2B.4C.3D.【答案】C【解析】如图为线性区域,区域内的点在直线上的投影构成了线段,即,而,由得,由得,.故选C.7.【2016年高考四川理数】设p:实数x,y满足,q:实数x,y满足则p是q的()(A)必要不充分条件(B)充分不必要条件(C)充要条件(D)既不充分也不必要条件【答案】A【解析】:画出可行域(如图所示),可知命题中不等式组表示的平面区域在命题中不等式表示的圆盘内,故选A.8.【2016高考江苏卷】已知实数满足,则的取值范围是▲.【答案】【解析】由图知原点到直线距离平方为最小值,为,原点到点距离平方为最大值,为,因此取值范围为9.【2016高考新课标1卷】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.【答案】【解析】设生产产品、产品分别为、件,利润之和为元,那么①目标函数.二元一次不等式组①等价于②作出二元一次不等式组②表示的平面区域(如图),即可行域.将变形,得,平行直线,当直线经过点时,取得最大值.解方程组,得的坐标.所以当,时,.故生产产品、产品的利润之和的最大值为元.10.【2015高考山东,理6】已知满足约束条件,若的最大值为4,则()(A)3(B)2(C)-2(D)-3【答案】B11.【2015高考新课标1,理15】若满足约束条件,则的最大值为.【答案】3【解析】作出可行域如图中阴影部分所示,由斜率的意义知,是可行域内一点与原点连线的斜率,由图可知,点A(1,3)与原点连线的斜率最大,故的最大值为3.12.【2015高考浙江,理14】若实数满足,则的最小值是.【答案】.【解析】表示圆及其内部,易得直线与圆相离,故,当时,,如下图所示,可行域为小的弓形内部,目标函数,则可知当,时,,当时,,可行域为大的弓形内部,目标函数,同理可知当,时,,综上所述,.【2017考试大纲】二元一次不等式组与简单线性规划问题(1)会从实际情境中抽象出二元一次不等式组.(2)了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.(3)会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.【三年高考命题回顾】纵观前三年各地高考试题,对二元一次不等式(组)与线性规划及简单应用这部分的考查,主要考查二元一次不等式(组)表示的平面区域、目标函数的最优解问题、与最优解相关的参数问题,高考中一般会以选填题形式考查.从近几年高考试题来看,试题难度较低,属于中低档试题,一般放在选择题的第5-7题或填空题的前两位.【2018年高考复习建议与高考命题预测】由前三年的高考命题形式可以看出,二元一次不等式(组)表示的平面区域(的面积),求目标函数的最...