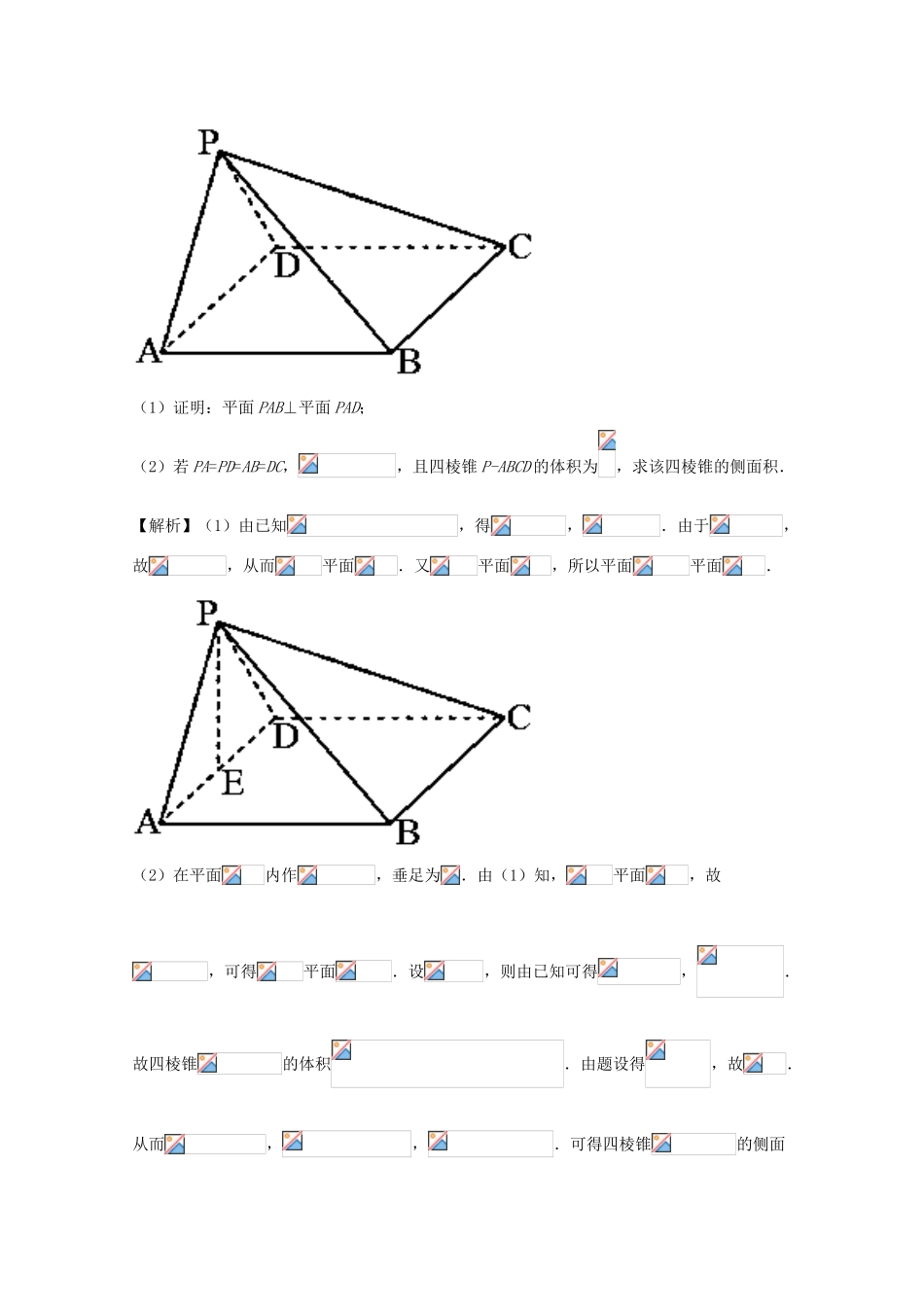
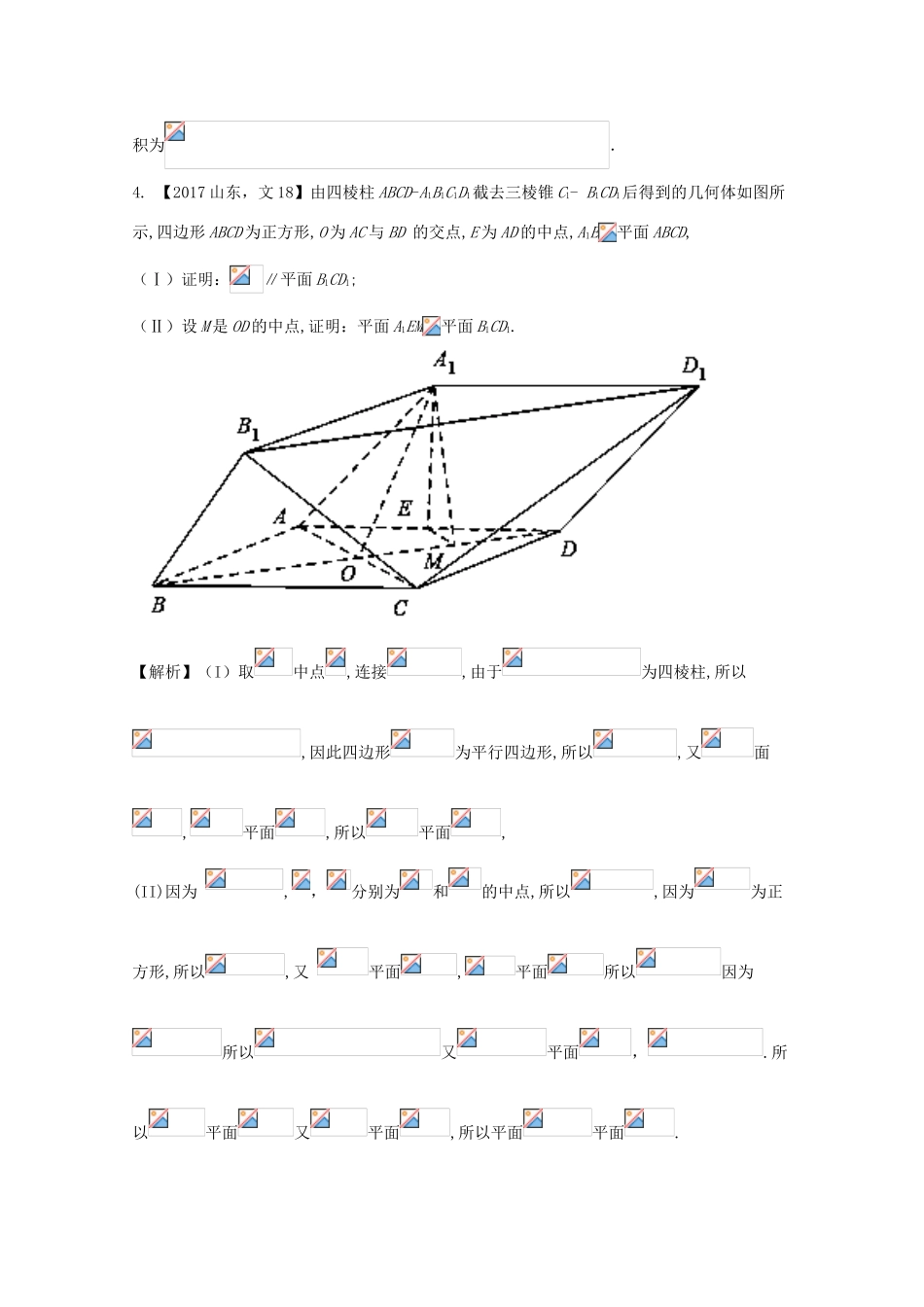
专题8.2点、直线、平面平行与垂直的判定与性质【三年高考】1.【2017课标1,文6】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是【答案】A【解析】由B,AB∥MQ,则直线AB∥平面MNQ;由C,AB∥MQ,则直线AB∥平面MNQ;由D,AB∥NQ,则直线AB∥平面MNQ.故A不满足,选A.2.【2017课标3,文10】在正方体中,E为棱CD的中点,则()A.B.C.D.【答案】C3.【2017课标1,文18】如图,在四棱锥P-ABCD中,AB//CD,且.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.【解析】(1)由已知,得,.由于,故,从而平面.又平面,所以平面平面.(2)在平面内作,垂足为.由(1)知,平面,故,可得平面.设,则由已知可得,.故四棱锥的体积.由题设得,故.从而,,.可得四棱锥的侧面积为.4.【2017山东,文18】由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E平面ABCD,(Ⅰ)证明:∥平面B1CD1;(Ⅱ)设M是OD的中点,证明:平面A1EM平面B1CD1.【解析】(I)取中点,连接,由于为四棱柱,所以,因此四边形为平行四边形,所以,又面,平面,所以平面,(II)因为,,分别为和的中点,所以,因为为正方形,所以,又平面,平面所以因为所以又平面,.所以平面又平面,所以平面平面.5.【2016高考浙江文数】已知互相垂直的平面交于直线l.若直线m,n满足m∥α,n⊥β,则()A.m∥lB.m∥nC.n⊥lD.m⊥n【答案】C【解析】由题意知,.故选C.6.【2016高考山东文数】已知直线a,b分别在两个不同的平面α,内,则“直线a和直线b相交”是“平面α和平面相交”的()(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件【答案】A【解析】“直线和直线相交”“平面和平面相交”,但“平面和平面相交”“直线和直线相交”,所以“直线和直线相交”是“平面和平面相交”的充分不必要条件,故选A.7.【2016高考山东文数】在如图所示的几何体中,D是AC的中点,EF∥DB.IFEHGBDCA(I)已知AB=BC,AE=EC.求证:AC⊥FB;(II)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.【解析】(Ⅰ))证明:因,所以与确定一个平面,连接,因为为的中点,所以;同理可得,又因为,所以平面,因为平面,。(Ⅱ)设的中点为,连,在中,是的中点,所以,又,所以;在中,是的中点,所以,又,所以平面平面,因为平面,所以平面.8.[2016高考新课标Ⅲ文数]如图,四棱锥中,平面,,,,为线段上一点,,为的中点.(I)证明平面;(II)求四面体的体积.【解析】(Ⅰ)由已知得,取的中点,连接,由为中点知,.又,故,四边形为平行四边形,于是.因为平面,平面,所以平面.9.【2015高考浙江,文4】设,是两个不同的平面,,是两条不同的直线,且,()A.若,则B.若,则C.若,则D.若,则【答案】A【解析】采用排除法,选项A中,平面与平面垂直的判定,故正确;选项B中,当时,可以垂直,也可以平行,也可以异面;选项C中,时,可以相交;选项D中,时,也可以异面.故选A.10.【2015高考北京,文18】如图,在三棱锥中,平面平面,为等边三角形,且,,分别为,的中点.(I)求证:平面;(II)求证:平面平面;(III)求三棱锥的体积.【解析】(Ⅰ)因为分别为,的中点,所以.又因为平面,所以平面.(Ⅱ)因为,为的中点,所以.又因为平面平面,且平面,所以平面.所以平面平面.(Ⅲ)在等腰直角三角形中,,所以.所以等边三角形的面积.又因为平面,所以三棱锥的体积等于.又因为三棱锥的体积与三棱锥的体积相等,所以三棱锥的体积为.11.【2015高考广东,文18】如图,三角形所在的平面与长方形所在的平面垂直,,,.(1)证明:平面;(2)证明:;(3)求点到平面的距离.【解析】(1)因为四边形是长方形,所以,因为平面,平面,所以平面(2)因为四边形是长方形,所以,因为平面平面,平面平面,平面,所以平面,因为平面,所以(3)取的中点,连结和,因为,所以,在中,,因为平面平面,平面平面,平面,所...