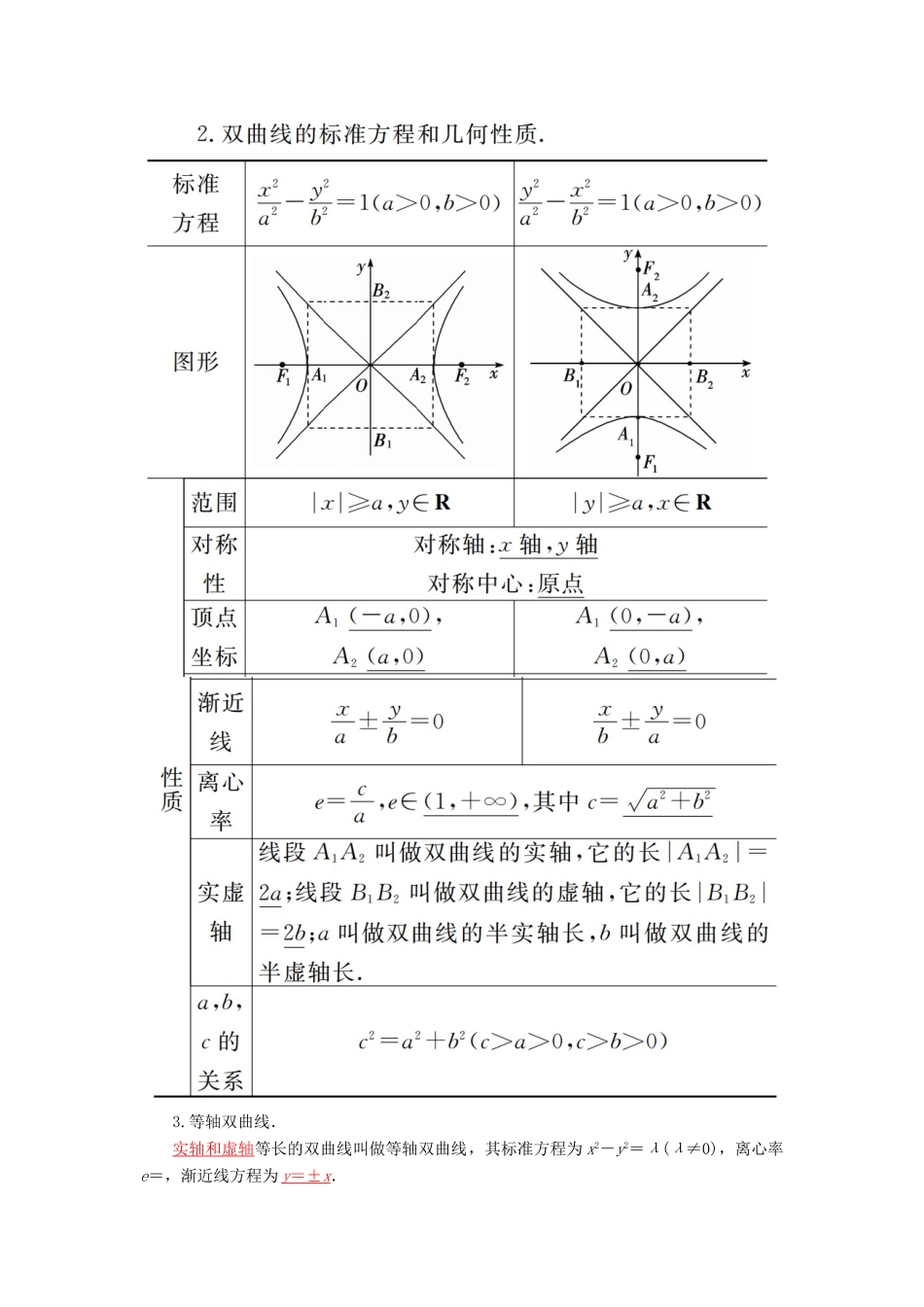
专题六解析几何第二讲椭圆、双曲线、抛物线1.椭圆的定义.平面内的动点的轨迹是椭圆必须满足的两个条件.(1)到两个定点F1,F2的距离的和等于常数2a.(2)2a>|F1F2|.1.双曲线的定义.平面内动点的轨迹是双曲线必须满足的两个条件:(1)到两个定点F1,F2的距离的差的绝对值等于常数2a.(2)2a<|F1F2|.3.等轴双曲线.实轴和虚轴等长的双曲线叫做等轴双曲线,其标准方程为x2-y2=λ(λ≠0),离心率e=,渐近线方程为y=±x.1.抛物线的定义.平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线,点F叫做抛物线的焦点,直线l叫做抛物线的准线.若二元方程f(x,y)=0是曲线C的方程,或曲线C是方程f(x,y)=0的曲线,则必须满足以下两个条件:1.曲线上点的坐标都是二元方程f(x,y)=0的解(纯粹性).2.以这个方程的解为坐标的点都是曲线C上的点(完备性).判断下面结论是否正确(请在括号中打“√”或“×”).(1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆.(×)(2)椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c(其中a为椭圆的长半轴长,c为椭圆的半焦距).(√)(3)椭圆的离心率e越大,椭圆就越圆.(√)(4)+=1(a>b>0)与+=1(a>b>0)的焦距相同.(√)(5)方程-=1(mn>0)表示焦点在x轴上的双曲线.(×)1.平面内到点A(0,1)、B(1,0)距离之和为2的点的轨迹为(A)A.椭圆B.一条射线C.两条射线D.一条线段解析:因为点到两定点AB距离之和为2>|AB|=,所以该点的轨迹为椭圆.故选A.2.以知F是双曲线-=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为9.解析:注意到A点在双曲线的两支之间,且双曲线右焦点为F′(4,0),于是由双曲线性质|PF|-|PF′|=2a=4,而|PA|+|PF′|≥|AF′|=5,两式相加得|PF|+|PA|≥9,当且仅当A、P、F′三点共线时等号成立.3.(2015·新课标Ⅰ卷)一个圆经过椭圆+=1的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为(x-)2+y2=.解析:由题意知a=4,b=2,上、下顶点的坐标分别为(0,2),(0,-2),右顶点的坐标为(4,0).由圆心在x轴的正半轴上知圆过点(0,2),(0,-2),(4,0)三点.设圆的标准方程为(x-m)2+y2=r2(0<m<4,r>0),则解得所以圆的标准方程为(x-)2+y2=.4.(2015·北京卷)已知双曲线-y2=1(a>0)的一条渐近线为x+y=0,则a=________.解析:双曲线-y2=1的渐近线为y=±,已知一条渐近线为x+y=0,即y=-x,因为a>0,所以=,所以a=.答案:一、选择题1.若椭圆+=1的离心率为,则实数m等于(A)A.或B.C.D.或解析:若m>2,则=,解得m=.若0<m<2,则=,解得m=.2.(2015·新课标Ⅱ卷)过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=(C)A.2B.8C.4D.10解析:设圆的方程为x2+y2+Dx+Ey+F=0,则解得∴圆的方程为x2+y2-2x+4y-20=0.令x=0,得y=-2+2或y=-2-2,∴M(0,-2+2),N(0,-2-2)或M(0,-2-2),N(0,-2+2),∴|MN|=4,故选C.3.(2015·福建卷)若双曲线E:-=1的左、右焦点分别为F1,F2,点P在双曲线E上,且|PF1|=3,则|PF2|等于(B)A.11B.9C.5D.34.已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为(A)A.B.C.(1,2)D.(1,-2)解析:如图,抛物线的焦点F(1,0),准线方程l:x=-1,点P到准线的距离为|PD|.由抛物线的定义知|PF|=|PD|,显然D,P,Q共线时,|PD|+|PQ|最小,即|PF|+|PQ|最小.此时yP=-1,代入抛物线方程知xp=,∴P.5.(2014·江西卷)过双曲线C:-=1的右顶点作x轴的垂线与C的一条渐近线相交于A.若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为(A)A.-=1B.-=1C.-=1D.-=1解析:因为C:-=1的渐近线为y=±x,所以A(a,b)或A(a,-b).因此OA=c=4,从而三角形OAC为正三角形,即tan60°=,a=2,b=2,双曲线C的方程为-=1.6.(2014·全国大纲卷)双曲线C:-=1(a>0,b>0)的离心率为2,焦点到渐近线的距离为,则C的焦距等于(C)A.2B.2C.4D.4解析:由已知可知渐...