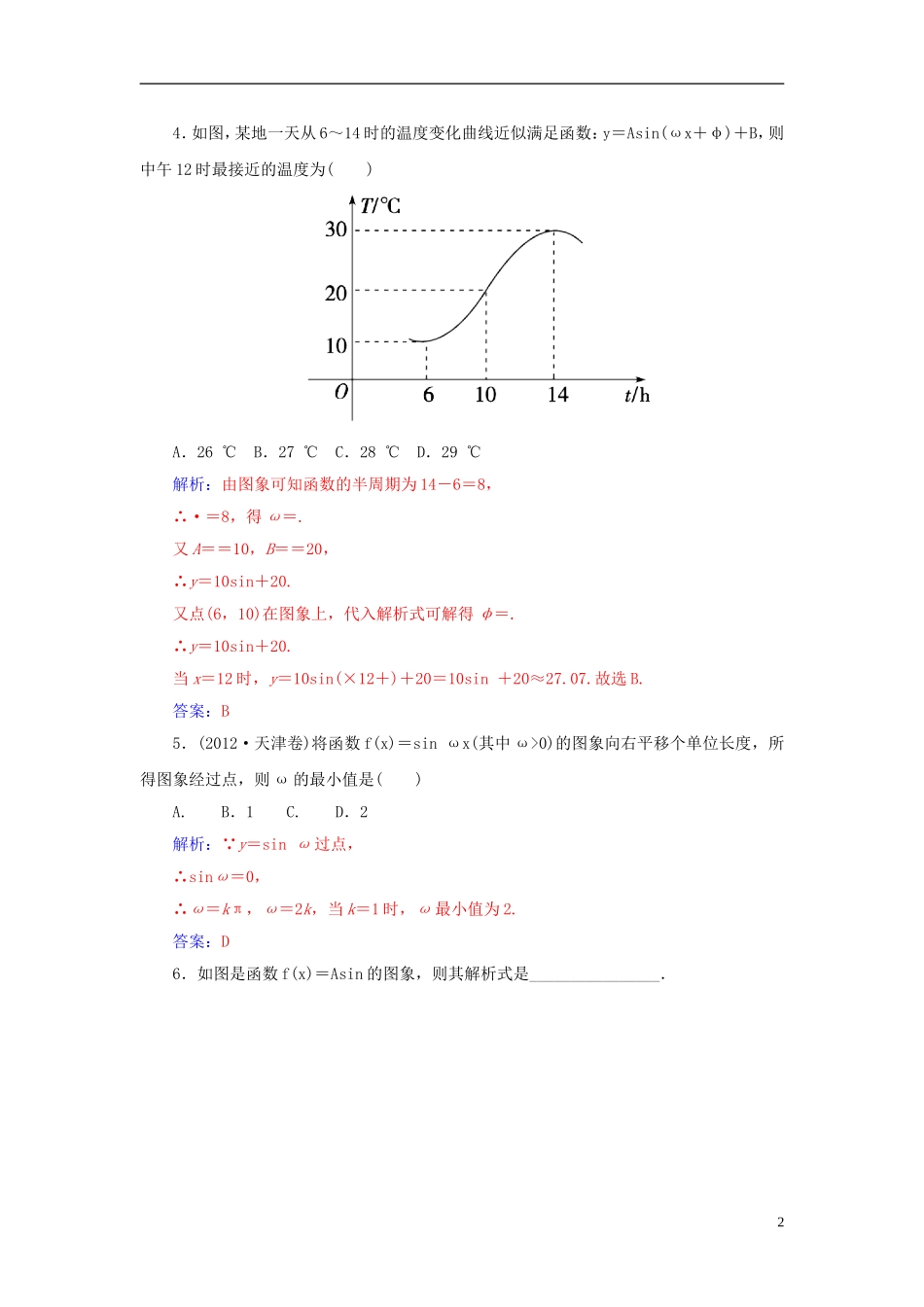
第六节函数y=Asin(ωx+φ)的图象及三角函数模型的应用题号12345答案1.(2013·山东卷)将函数y=sin(2x+φ)的图象沿x轴向左平移个单位后,得到一个偶函数的图象,则φ的一个可能取值为()A.B.C.0D.-解析:把函数y=sin(2x+φ)沿x轴向左平移个单位后得到函数y=sin=sin为偶函数,则φ=.故选B.答案:B2.将函数y=sin的图象向右平移个单位,再向上平移2个单位所得图象对应的函数解析式是()A.y=sin+2B.y=sin+2C.y=sin-2D.y=sin-2解析:y=sin+2=sin+2,故选B.答案:B3.如图是周期为2π的三角函数y=f(x)的图象,那么f(x)可以写成()A.f(x)=sin(1+x)B.f(x)=sin(-1-x)C.f(x)=sin(x-1)D.f(x)=sin(1-x)解析:设y=sin(x+φ),点(1,0)为五点法作图的第三点,∴由sin(1+φ)=0⇒1+φ=π,φ=π-1,∴y=sin(x+π-1)=sin(1-x).答案:D14.如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+B,则中午12时最接近的温度为()A.26℃B.27℃C.28℃D.29℃解析:由图象可知函数的半周期为14-6=8,∴·=8,得ω=.又A==10,B==20,∴y=10sin+20.又点(6,10)在图象上,代入解析式可解得φ=.∴y=10sin+20.当x=12时,y=10sin(×12+)+20=10sin+20≈27.07.故选B.答案:B5.(2012·天津卷)将函数f(x)=sinωx(其中ω>0)的图象向右平移个单位长度,所得图象经过点,则ω的最小值是()A.B.1C.D.2解析:∵y=sinω过点,∴sinω=0,∴ω=kπ,ω=2k,当k=1时,ω最小值为2.答案:D6.如图是函数f(x)=Asin的图象,则其解析式是________________.2解析:依题意,A=3,T=π,故ω==2,故f(x)=3sin(2x+φ),因为f=3,故3sin=3,即+φ=+2kπ(k∈Z),故φ=+2kπ(k∈Z),因为|φ|<,故φ=,所以f(x)=3sin.答案:f(x)=3sin7.当函数y=sinx-cosx(0≤x<2π)取得最大值时,x=________.解析:由y=sinx-cosx=2sin,∵0≤x<2π,∴x-∈,当x-=,即x=时,函数取得最大值为2.答案:8.设函数f(x)=sin,现有下列结论:①f(x)的图象关于直线x=对称;②f(x)的图象关于点对称;③把f(x)的图象向左平移个单位长度,得到一个偶函数的图象;④f(x)的最小正周期为π,且在上为增函数.其中正确的结论有____________(把你认为正确的序号都填上).答案:③9.已知函数f(x)=cos2x+sinxcosx,x∈R.(1)求f的值;(2)若sinα=,且α∈,求f.解析:(1)f=cos2+sincos=+×=.(2)f(x)=cos2x+sinxcosx=+sin2x=+(sin2x+cos2x)3=+sin,f=+sin=+sin=+.因为sinα=,且α∈,所以cosα=-,所以f=+=.10.已知函数f(x)=Asin(A>0,x∈R)的最小值为-2.(1)求f(0);(2)若函数f(x)的图象向左平移φ(φ>0)个单位长度,得到的曲线关于y轴对称,求φ的最小值.解析:(1)因为函数f(x)=Asin(A>0,x∈R)的最小值为-2,所以A=2,f(x)=2sin,f(0)=2sin=1.(2)函数f(x)的图象向左平移φ(φ>0)个单位长度,可得y=2sin.因为y=2sin的图象关于y轴对称,所以2(0+φ)+=+kπ,k∈Z.解得φ=-+,k∈Z,因为φ>0,所以φ的最小值为.4