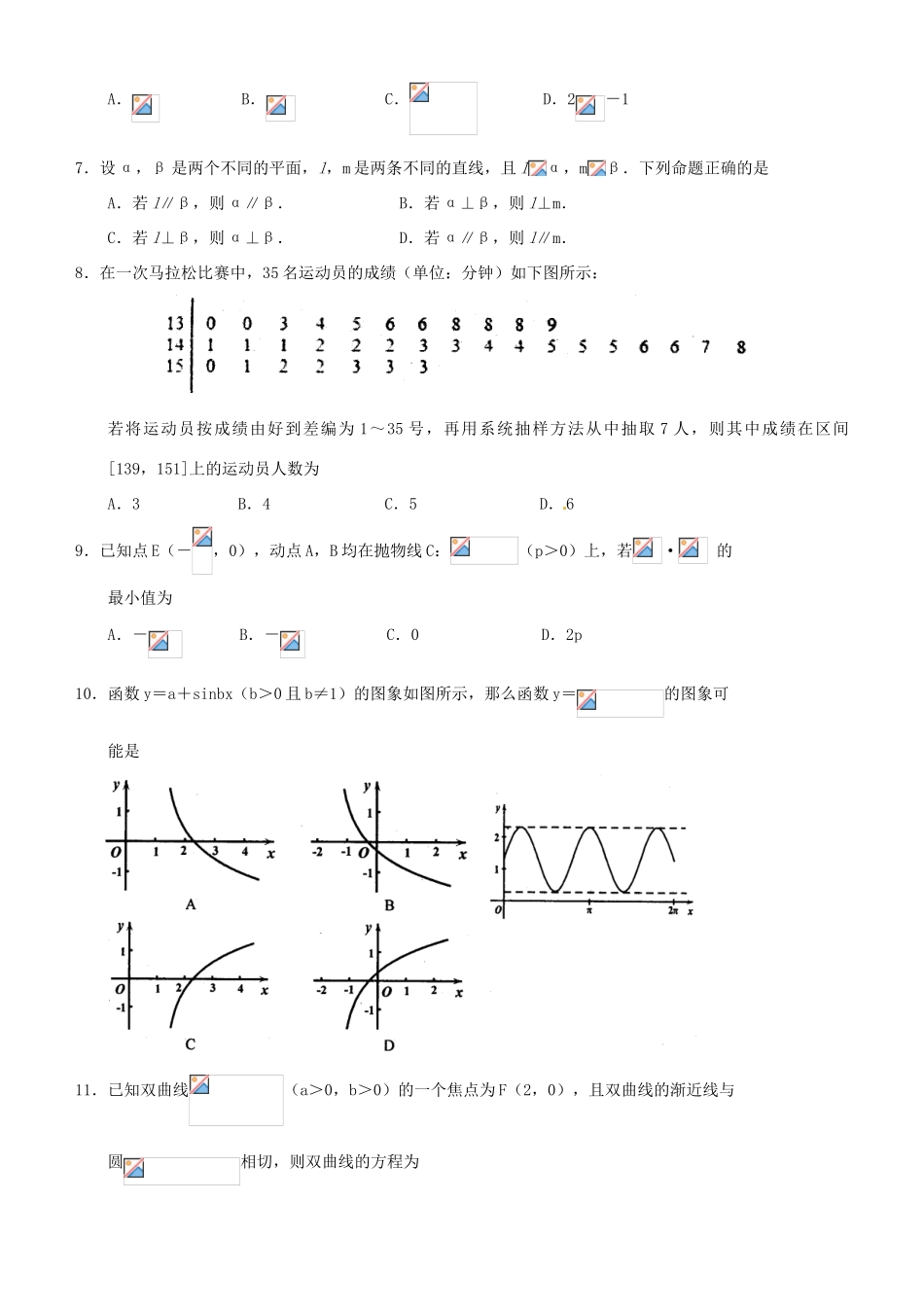
平顶山市2016届高三年级第二次调研考试高三文科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答题前,考生务必先将自己的姓名、准考证号填写在本试卷和答题卡相应位置上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上.2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案的标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案答在答题卡上,写在本试卷上无效。4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={0,1},集合B={x|x>a},若A∩B=,则实数a的范围是A.a≤1B.a≥1C.a≥0D.a≤02.复数z满足z·i=3-i,则在复平面内,复数z对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.关于函数f(x)=和g(x)=,下列说法中正确的是A.都是奇函数B.都是偶函数C.函数f(x)的值域为RD.函数g(x)的值域为R4.如右图所示,程序框图(算法流程图)的输出结果是A.B.C.D.5.等差数列{}的公差为3,若a2,a4,a6成等比数列,则{}的前2n项=A.3n(2n-1)B.3n(2n+1)C.D.6.4sin40°-tan40°的值为A.B.C.D.2-17.设α,β是两个不同的平面,l,m是两条不同的直线,且lα,mβ.下列命题正确的是A.若l∥β,则α∥β.B.若α⊥β,则l⊥m.C.若l⊥β,则α⊥β.D.若α∥β,则l∥m.8.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)如下图所示:若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数为A.3B.4C.5D.69.已知点E(-,0),动点A,B均在抛物线C:(p>0)上,若·的最小值为A.-B.-C.0D.2p10.函数y=a+sinbx(b>0且b≠1)的图象如图所示,那么函数y=的图象可能是11.已知双曲线(a>0,b>0)的一个焦点为F(2,0),且双曲线的渐近线与圆相切,则双曲线的方程为A.B.C.D.12.设函数f(x)=,若f(f())=4,则b等于A.1B.C.D.第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第2l题为必考题,每个试题考生都必答.第22题~24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,共20分.13.已知平面向量a与b的夹角为,|a|=,|b|=1,则|a-b|=________.14.满足的约束条件,则z=x+2y的最大值为_____________.15.如果a,b满足ab=a+b+3,那么ab的取值范围是______________16.椭圆(a>b>0)的右焦点F(c,0)关于直线y=x的对称点M在椭圆上,则椭圆的离心率是____________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.(Ⅰ)求BD的长;(Ⅱ)求sin∠CBD的值.18.(本小题满分12分)我市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100],并绘制出频率分布直方图,如图所示.(Ⅰ)求频率分布直方图中的a值;从该市随机选取一名学生,试估计这名学生参加考试的成绩低于90分的概率;(Ⅱ)设A,B,C三名学生的考试成绩在区间[80,90)内,M,N两名学生的考试成绩在区间[60,70)内,现从这5名学生中任选两人参加座谈会,求学生M,N至少有一人被选中的概率;(Ⅲ)试估计样本的中位数落在哪个分组区间内(只需写出结论).(注:将频率视为相应的概率)19.(本小题满分12分)如图,在四棱锥S—ABCD中,底面ABCD是平行四边形,侧面SBC是正三角形,点E是SB的中点,且AE⊥平面SBC.(Ⅰ)证明SD∥平面ACE;(Ⅱ)若AB⊥AS,BC=2,求点S到平面ABC的距离.20.(本小题满分12分)已知圆C的圆心为C(m,0),m<3,半径为,圆C与离心率e>的椭圆E:(a>b>0...