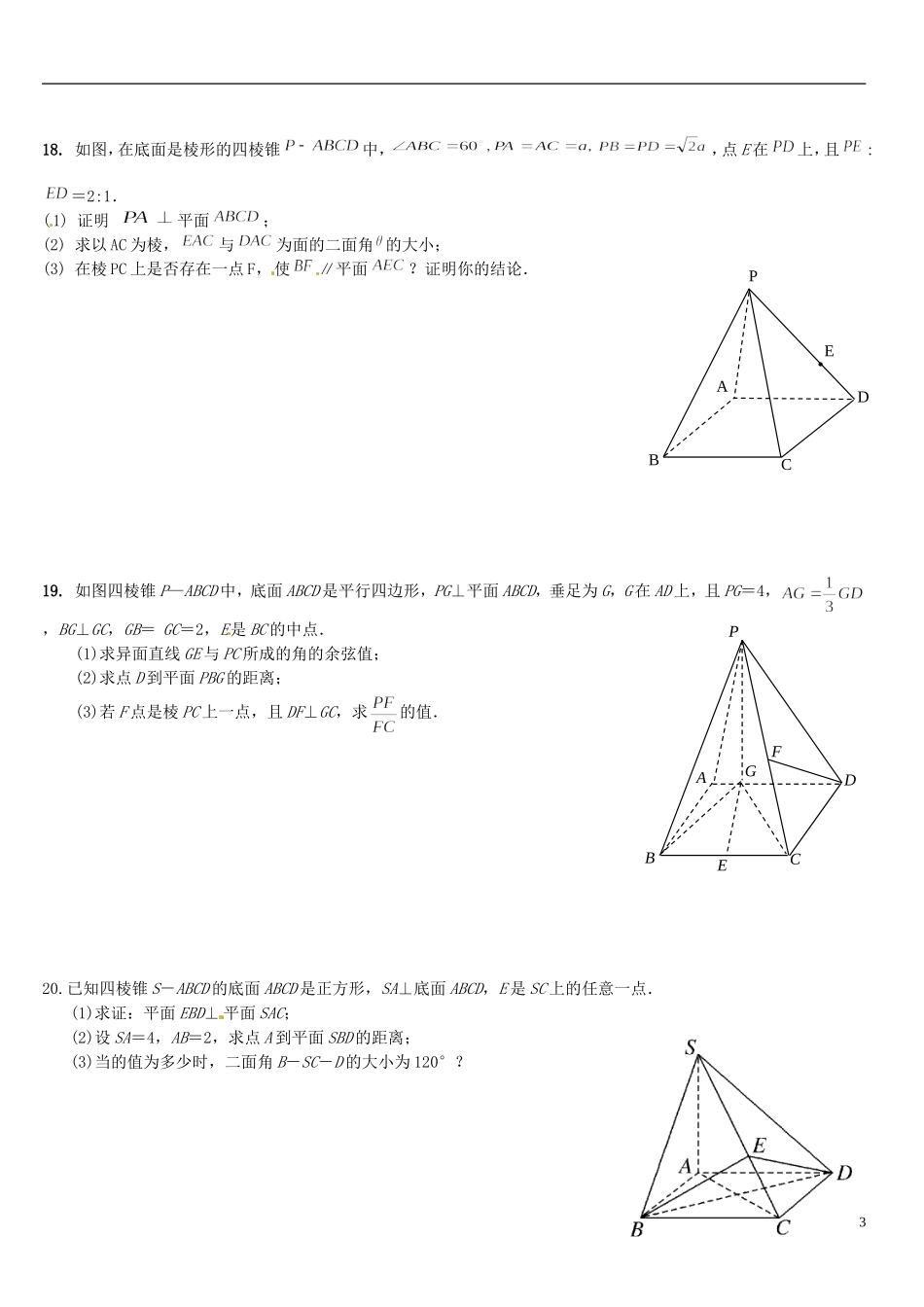
一、四川省木里县中学高三数学总复习数学立体几何练习题新人教A版二、选择题:1.如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是()A.相交B.平行C.垂直D.不能确定2.将正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,E是CD中点,则的大小为()A.B.C.D.3.PA,PB,PC是从P引出的三条射线,每两条的夹角都是60º,则直线PC与平面PAB所成的角的余弦值为()A.B。C。D。4.正方体ABCD—A1B1C1D1中,E、F分别是AA1与CC1的中点,则直线ED与D1F所成角的余弦值是A.B。C。D。5.在棱长为2的正方体中,O是底面ABCD的中心,E、F分别是、AD的中点,那么异面直线OE和所成的角的余弦值等于()A.B.C.D.6.在正三棱柱ABC-A1B1C1中,若AB=2,AA1=1,则点A到平面A1BC的距离为()A.B.C.D.7.在正三棱柱ABC-A1B1C1中,若AB=BB1,则AB1与C1B所成的角的大小为()A.60ºB.90ºC.105ºD.75º8.设E,F是正方体AC1的棱AB和D1C1的中点,在正方体的12条面对角线中,与截面A1ECF成60°角的对角线的数目是()A.0B.2C.4D.6二、填空题:本大题共6小题,每小题5分,共30分.9.在正方体ABCD-A1B1C1D1中,M、N分别为棱AA1和BB1的中点,则sin〈CM�,1DN�〉的值为_________.10.如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是.11.正四棱锥P-ABCD的所有棱长都相等,E为PC中点,则直线AC与截面BDE所成的角为.12.已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的正弦值为.13.已知边长为的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面过PF且与AE平行,则AE与平面间的距离为.14.棱长都为2的直平行六面体ABCD—A1B1C1D1中,∠BAD=60°,则对角线A1C与侧面DCC1D1所成角的余弦值为________.1ABMDCABCDP三、解答题:15.如图,直三棱柱,底面中,CA=CB=1,,棱,M、N分别A1B1、A1A是的中点.(1)求BM的长;(2)求的值;(3)求证:.16.如图,三棱锥P—ABC中,PC平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD平面PAB.(1)求证:AB平面PCB;(2)求异面直线AP与BC所成角的大小;(3)求二面角C-PA-B的大小的余弦值.17.如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.(1)试建立适当的坐标系,并写出点P、B、D的坐标;(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的余弦值大小.2QPDCBAxyzB1C1A1CBAMN18.如图,在底面是棱形的四棱锥中,,点E在上,且:=2:1.(1)证明平面;(2)求以AC为棱,与为面的二面角的大小;(3)在棱PC上是否存在一点F,使∥平面?证明你的结论.19.如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,,BG⊥GC,GB=GC=2,E是BC的中点.(1)求异面直线GE与PC所成的角的余弦值;(2)求点D到平面PBG的距离;(3)若F点是棱PC上一点,且DF⊥GC,求的值.20.已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.(1)求证:平面EBD⊥平面SAC;(2)设SA=4,AB=2,求点A到平面SBD的距离;(3)当的值为多少时,二面角B-SC-D的大小为120°?3CDBAPEPAGBCDFEABCDPxyz立体几何训练题答案一、选择题题号12345678答案BDDADBBC二、填空题9.10.11.45°12.13.14三、解答题15解析:以C为原点建立空间直角坐标系.(1)依题意得B(0,1,0),M(1,0,1)..(2)依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2)..(3)证明:依题意得C1(0,0,2),N.16.解析:(1) PC⊥平面ABC,平面ABC,∴PCAB. CD平面PAB,平面PAB,∴CDAB.又,∴AB平面PCB.(2由(I)AB平面PCB, PC=AC=2,又 AB=BC,可求得BC=.以B为原点,如图建立坐标系.则A(0,,0),B(0,0,0),C(,0,0),P(,0,2).=(,-,2),=(,0,0).则=×+0+0=2.===.∴异面直线AP与BC所成的角为.(3)设平面PAB的法向量为m=(x,y,z).=(0,-,0),=(,-,2),则即解得令z=-1,得m=(,0,-1)....