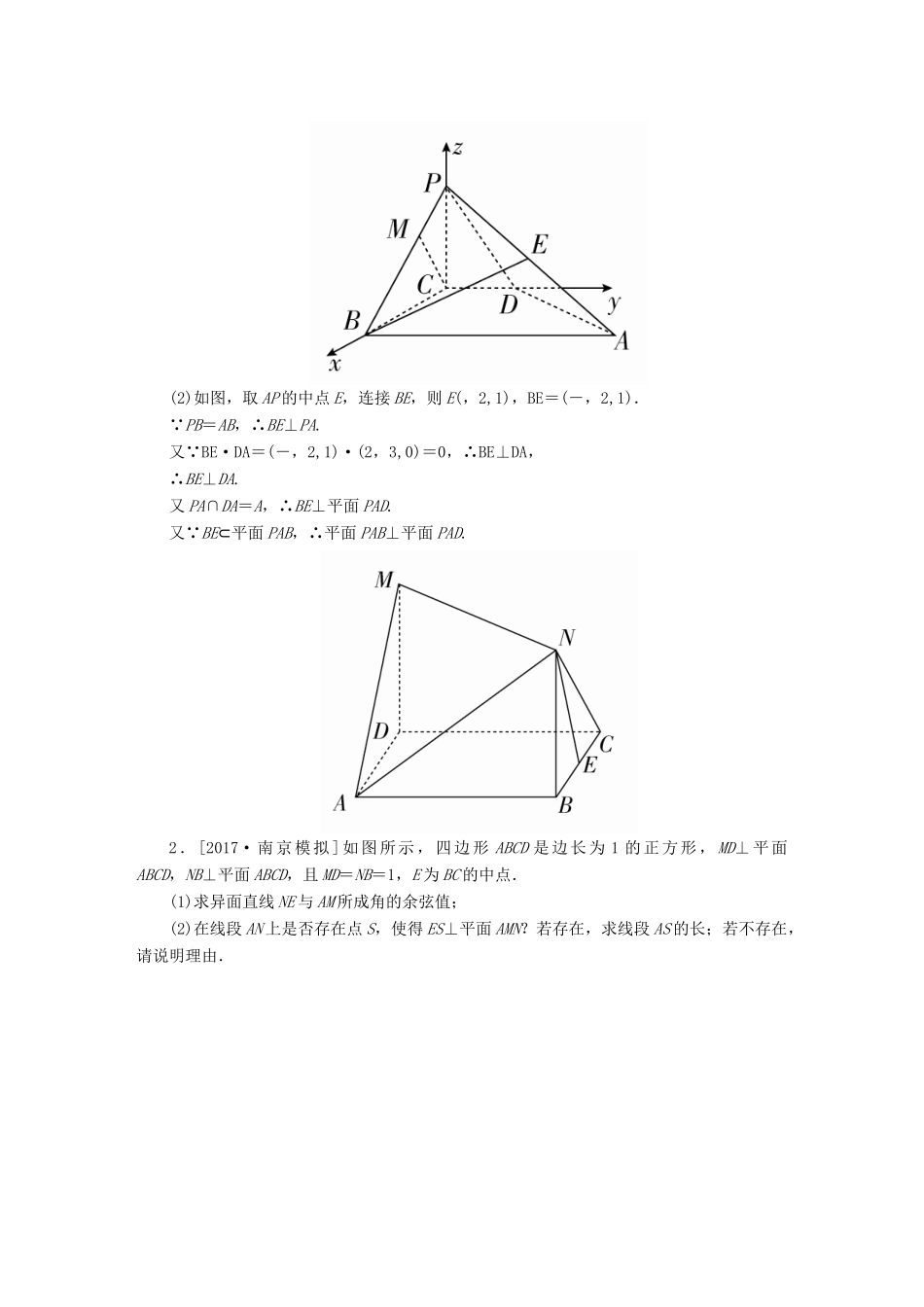
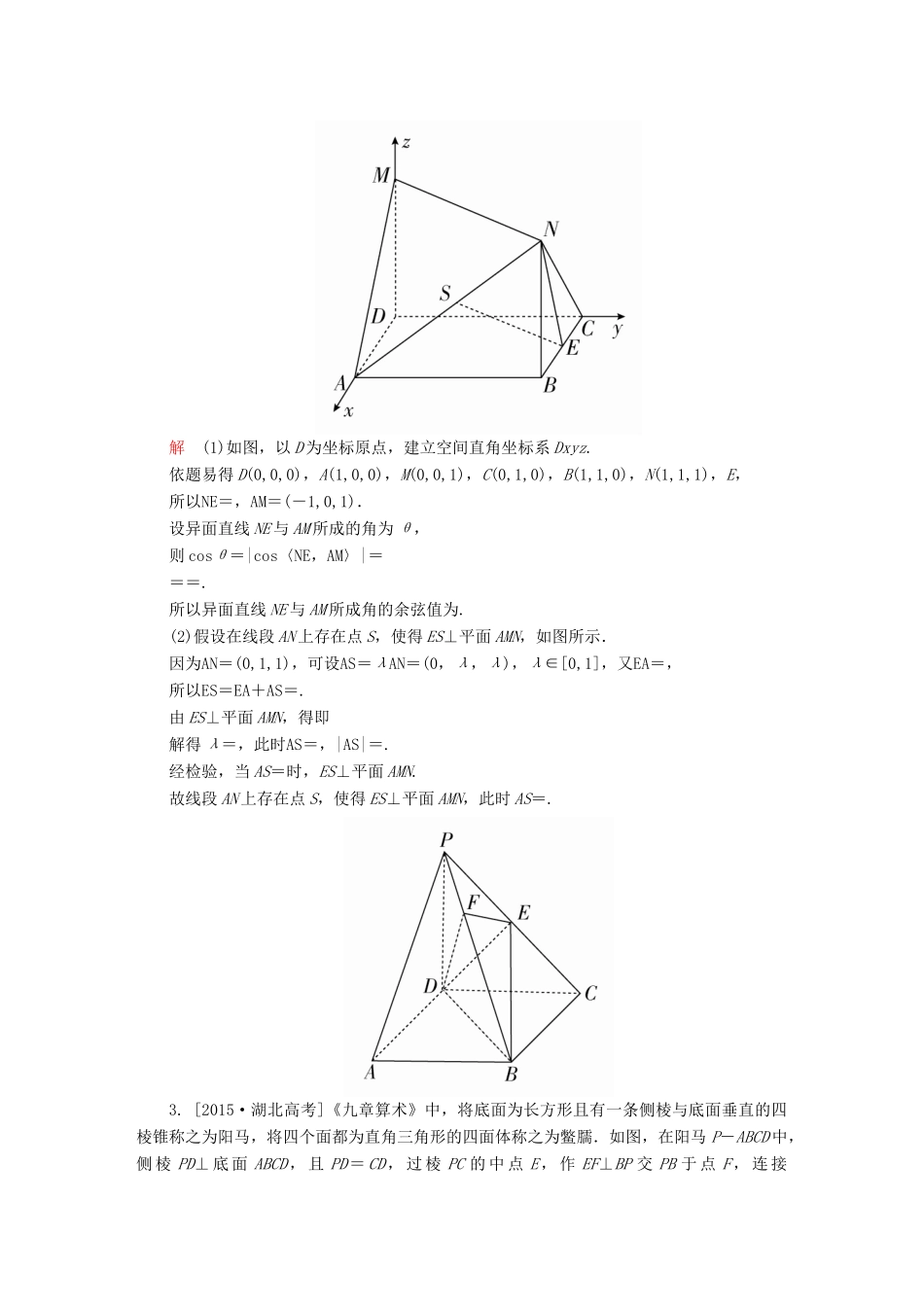
解答题专项训练四1.[2017·佛山模拟]如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.求证:(1)CM∥平面PAD;(2)平面PAB⊥平面PAD.证明(1)以C为坐标原点,CB为x轴,CD为y轴,CP为z轴建立如图所示的空间直角坐标系Cxyz. PC⊥平面ABCD,∴∠PBC为PB与平面ABCD所成的角,∴∠PBC=30°. PC=2,∴BC=2,PB=4,∴D(0,1,0),B(2,0,0),A(2,4,0),P(0,0,2),M,∴DP=(0,-1,2),DA=(2,3,0),CM=.(1)设n=(x,y,z)为平面PAD的一个法向量,由即令y=2,得n=(-,2,1). n·CM=-×+2×0+1×=0,∴n⊥CM.又CM⊄平面PAD,∴CM∥平面PAD.(2)如图,取AP的中点E,连接BE,则E(,2,1),BE=(-,2,1). PB=AB,∴BE⊥PA.又 BE·DA=(-,2,1)·(2,3,0)=0,∴BE⊥DA,∴BE⊥DA.又PA∩DA=A,∴BE⊥平面PAD.又 BE⊂平面PAB,∴平面PAB⊥平面PAD.2.[2017·南京模拟]如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.(1)求异面直线NE与AM所成角的余弦值;(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.解(1)如图,以D为坐标原点,建立空间直角坐标系Dxyz.依题易得D(0,0,0),A(1,0,0),M(0,0,1),C(0,1,0),B(1,1,0),N(1,1,1),E,所以NE=,AM=(-1,0,1).设异面直线NE与AM所成的角为θ,则cosθ=|cos〈NE,AM〉|===.所以异面直线NE与AM所成角的余弦值为.(2)假设在线段AN上存在点S,使得ES⊥平面AMN,如图所示.因为AN=(0,1,1),可设AS=λAN=(0,λ,λ),λ∈[0,1],又EA=,所以ES=EA+AS=.由ES⊥平面AMN,得即解得λ=,此时AS=,|AS|=.经检验,当AS=时,ES⊥平面AMN.故线段AN上存在点S,使得ES⊥平面AMN,此时AS=.3.[2015·湖北高考]《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥BP交PB于点F,连接DE,DF,BD,BE.(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑?若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(2)若平面DEF与平面ABCD所成二面角的大小为,求的值.解(1)证明:如图,以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0),PB=(λ,1,-1),点E是PC的中点,所以E,DE=,于是PB·DE=0,即PB⊥DE.又已知EF⊥PB,而DE∩EF=E,所以PB⊥平面DEF.因PC=(0,1,-1),DE·PC=0,则DE⊥PC,所以DE⊥平面PBC.由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.(2)由PD⊥平面ABCD,所以DP=(0,0,1)是平面ABCD的一个法向量;由(1)知PB⊥平面DEF,所以BP=(-λ,-1,1)是平面DEF的一个法向量.若平面DEF与平面ABCD所成二面角的大小为,则cos===,解得λ=.所以==.故当平面DEF与平面ABCD所成二面角的大小为时,=.4.如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.(1)求证:平面ABB1A1⊥平面ABC;(2)求直线B1D与平面ACC1A1所成角的正弦值.解(1)证明:取AB的中点为O,连接OD,OB1,因为B1B=B1A,所以OB1⊥AB.又AB⊥B1D,OB1∩B1D=B1,所以AB⊥平面B1OD.因为OD⊂平面B1OD,所以AB⊥OD.由已知,BC⊥BB1,又OD∥BC,所以OD⊥BB1.因为AB∩BB1=B,所以OD⊥平面ABB1A1.又OD⊂平面ABC,所以平面ABC⊥平面ABB1A1.(2)由(1)知,OB,OD,OB1两两垂直,以O为坐标原点,OB为单位长度,建立如图所示的空间直角坐标系Oxyz.由题设知B1(0,0,),D(0,1,0),A(-1,0,0),C(1,2,0),C1(0,2,).则B1D=(0,1,-),AC=(2,2,0),CC1=(-1,0,).设平面ACC1A1的法向量为m=(x,y,z),则m·AC=0,m·CC1=0,即x+y=0,-x+z=0,可取m=(,-,1).设直线B1D与...