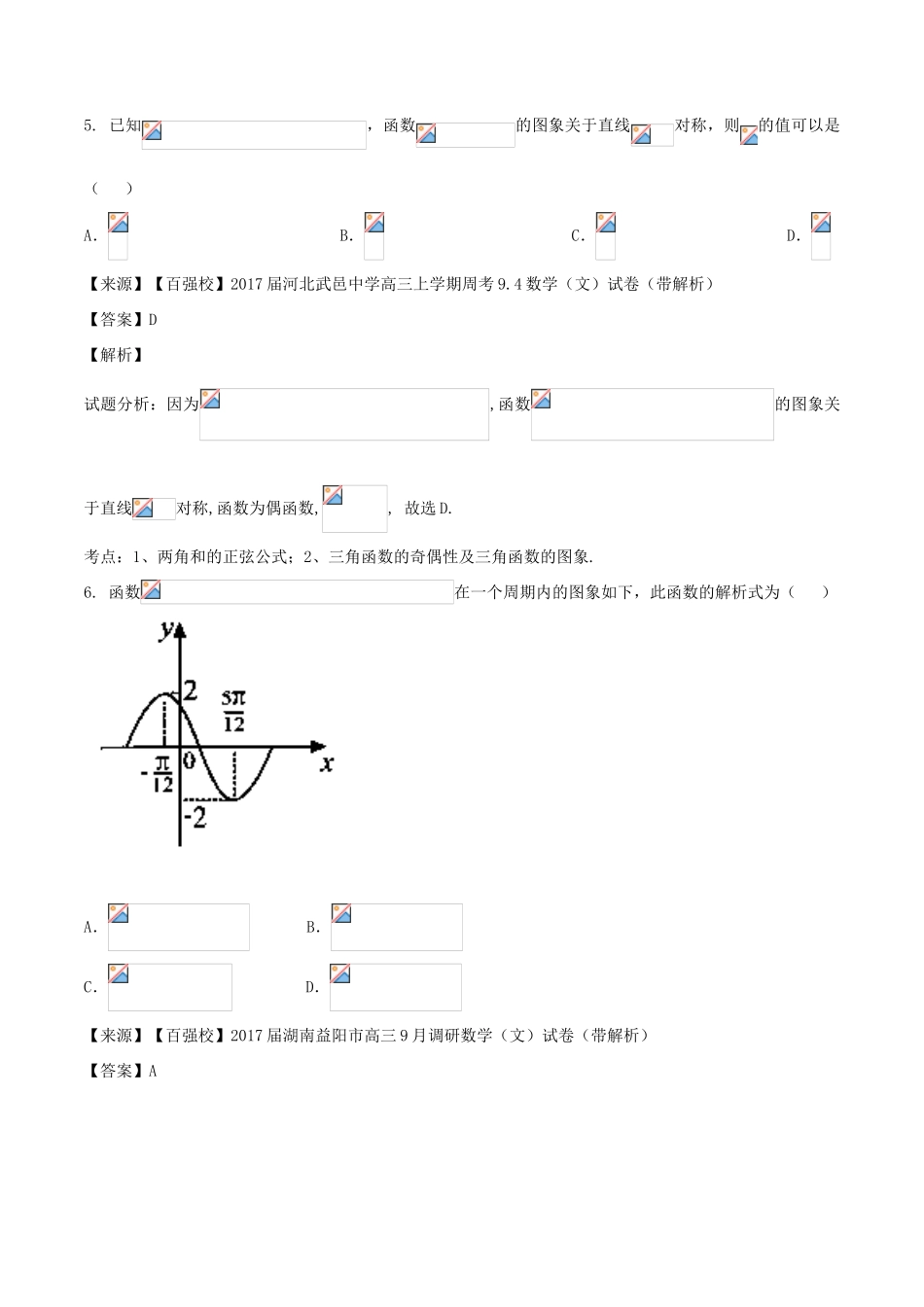
专题3.1三角函数的图像和性质(测试时间:120分钟满分:150分)一、选择题(共12小题,每题5分,共60分)1.【2018广东广州一模】已知函数是奇函数,直线与函数的图象的两个相邻交点的横坐标之差的绝对值为,则().A.在上单调递减B.在上单调递减C.在上单调递增D.在上单调递增【答案】D【点睛】函数的性质(1).(2)周期(3)由求对称轴(4)由求增区间;由求减区间2.函数对任意都有,则等于()A.或B.或C.D.或【答案】B.【解析】试题分析:由可知函数图象关于直线对称,则在处取得最值,所以,故选B.考点:三角函数的性质.3.函数在区间[0,π]上的一个单调递减区间是()A.B.C.D.【答案】B【解析】试题分析:令,解得:,当k=0时得:。考点:三角函数单调性.4.要得到函数的图象,只需要将函数的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【来源】【百强校】2017届广东海珠区高三上学期调研测试一数学文试卷(带解析)【答案】A【解析】考点:三角函数的平移变换.5.已知,函数的图象关于直线对称,则的值可以是()A.B.C.D.【来源】【百强校】2017届河北武邑中学高三上学期周考9.4数学(文)试卷(带解析)【答案】D【解析】试题分析:因为,函数的图象关于直线对称,函数为偶函数,,故选D.考点:1、两角和的正弦公式;2、三角函数的奇偶性及三角函数的图象.6.函数在一个周期内的图象如下,此函数的解析式为()A.B.C.D.【来源】【百强校】2017届湖南益阳市高三9月调研数学(文)试卷(带解析)【答案】A考点:三角函数的图象和性质.7.【2018陕西西安长安区联考】把函数的图象上个点的横坐标缩短到原来的(纵坐标不变),再将图象向右平移个单位,那么所得图象的一个对称中心为A.B.C.D.【答案】D【解析】根据题意函数)的图象上个点的横坐标缩短到原来的(纵坐标不变),可得,再将图象向右平移个单位,可得:令可得:当时,可得对称中点为故选D.8.设函数,则f(x)=sin(2x+)+cos(2x+),则()A.y=f(x)在(0,)单调递增,其图象关于直线x=对称B.y=f(x)在(0,)单调递增,其图象关于直线x=对称C.y=f(x)在(0,)单调递减,其图象关于直线x=对称D.y=f(x)在(0,)单调递减,其图象关于直线x=对称【答案】D【解析】考点:1.辅助角公式;2.三角函数的性质。9.【2018云南昆明一中一模】已知函数(),且,当取最小值时,以下命题中假命题是()A.函数的图象关于直线对称B.是函数的一个零点C.函数的图象可由的图象向左平移个单位得到D.函数在上是增函数【答案】C将函数的图象向左平移个单位得到的图象,所以C为假;由复合函数单调性可得在上是增函数,所以D为真,选C.【点睛】函数的性质(1).(2)周期(3)由求对称轴(4)由求增区间;由求减区间10.同时具有性质①最小正周期是;②图象关于直线对称;③在上是增函数的一个函数为()A.B.C.D.【来源】【百强校】2016届宁夏六盘山高级中学高三五模考试数学(文)试卷(带解析)【答案】C【解析】试题分析:周期是的只有,,当时,,因此C是增,B是减,故选C.考点:三角函数的周期,单调性,对称性.11.函数的定义域为,值域为,则的最大值是()(A)(B)(C)(D)【答案】B【解析】考点:正弦函数的值域.12.设ω>0,若函数f(x)=2sinωx在[-]上单调递增,则ω的取值范围是()A.B.C.D.【答案】D【解析】利用正弦函数的性质,函数在区间上单调递增,因此由题设,即故有.考点:三角函数性质的应用二.填空题(共4小题,每小题5分,共20分)13.在函数①,②,③,④中,最小正周期为的所有函数为.【答案】①②③【解析】试题分析:①,②的周期为,所以的周期为,③的周期为,④的周期为考点:三角函数周期性14.已知函数在区间[,]上的最小值是-2,则的最小值.【答案】【解析】函数在区间上的最小值是,则的取值范围是,∴或,∴的最小值为考点:三角函数的性质15.【2018上海交大附中摸底】设函数,其中,若,且的最小正周期大于,则__________.【答案】取,得,所以.16.已知函数(其中)的图象关于点成中心对称,且与点相邻的一个最低点为,则对于下列判断:①...