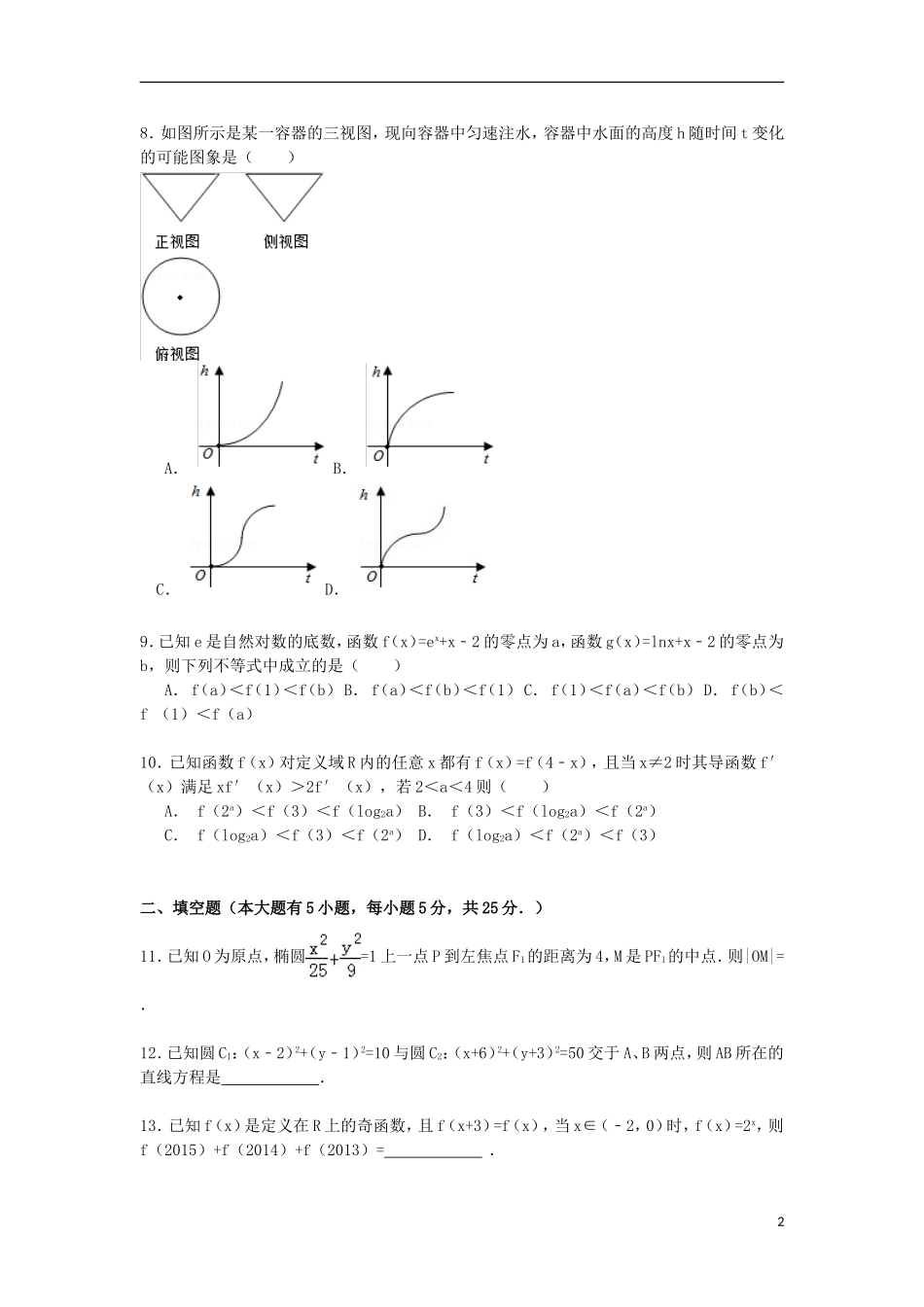
2014-2015学年山东省青岛市胶州一中高三(上)12月质量检测数学试卷(文科)一、选择题(本大题有10小题,每小题5分,共50分.)1.若a,b,c∈R,a>b,则下列不等式成立的是()A.B.C.a2>b2D.a|c|>b|c|2.下列说法一定正确的是()A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况B.一枚硬币掷一次得到正面的概率是,那么掷两次一定会出现一次正面的情况C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元D.随机事件发生的概率与试验次数无关3.已知向量=(2,3),=(﹣1,2),若m+n与﹣2共线,则等于()A.﹣B.C.﹣2D.24.已知函数f(x)=x2﹣bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列{}的前n项和为Sn,则S2014的值为()A.B.C.D.5.如表是某厂1~4月份用水量(单位:百吨)的一组数据:月份x1234用水量y4.5432.5由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是,则a等于()A.5.1B.5.2C.5.25D.5.46.已知函数,若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数,则该函数有两个极值点的概率为()A.B.C.D.7.在△ABC中,a=80,b=100,A=45°,则此三角形解的情况是()A.一解B.两解C.一解或两解D.无解18.如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h随时间t变化的可能图象是()A.B.C.D.9.已知e是自然对数的底数,函数f(x)=ex+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式中成立的是()A.f(a)<f(1)<f(b)B.f(a)<f(b)<f(1)C.f(1)<f(a)<f(b)D.f(b)<f(1)<f(a)10.已知函数f(x)对定义域R内的任意x都有f(x)=f(4﹣x),且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4则()A.f(2a)<f(3)<f(log2a)B.f(3)<f(log2a)<f(2a)C.f(log2a)<f(3)<f(2a)D.f(log2a)<f(2a)<f(3)二、填空题(本大题有5小题,每小题5分,共25分.)11.已知O为原点,椭圆=1上一点P到左焦点F1的距离为4,M是PF1的中点.则|OM|=.12.已知圆C1:(x﹣2)2+(y﹣1)2=10与圆C2:(x+6)2+(y+3)2=50交于A、B两点,则AB所在的直线方程是.13.已知f(x)是定义在R上的奇函数,且f(x+3)=f(x),当x∈(﹣2,0)时,f(x)=2x,则f(2015)+f(2014)+f(2013)=.214.已知如图是一个空间几何体的三视图,则该几何体的外接球的表面积为.15.已知命题:①若a≤b,则ac2≤bc2;②“设a,b∈R,若a+b≠6,则a≠3或b≠3”是一个真命题;③在△ABC中,cos2A<cos2B的充要条件是A>B;④“所有的素数都是偶数”的否定是“所有的素数不都是偶数”;⑤“P∨Q为真命题”是“¬P为假命题”的必要不充分条件.其中正确命题的序号是.三、解答题(共75分)16.甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?17.已知函数f(x)=,其中向量=(sinωx+cosωx,cosωx),=(cosωx﹣sinωx,2sinωx),ω>0,若f(x)的图象上相邻两个对称中心的距离大于等于π.(1)求ω的取值范围;(2)在△ABC中,a,b,c分别是角A,B,C的对边,a=,当ω最大时,f(A)=1,求△ABC的面积最大值.18.已知递增等比数列{an}的前n项和为Sn,a1=1,且S3=2S2+1.(1)求数列{an}的通项公式;(2)若数列{bn}满足bn=2n﹣1+an(n∈N*),且{bn}的前n项和Tn.求证:Tn≥2.319.如图,矩形ABCD中,AB=3,BC=4.E,F分别在线段BC和AD上,EF∥AB,将矩形ABEF沿EF折起.记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.(Ⅰ)求证:NC∥平面MFD;(Ⅱ)若EC=3,求证:ND⊥FC;(Ⅲ)求四面体NFEC体积的最大值.20...