第四节正弦型函数的图象及应用VIP免费

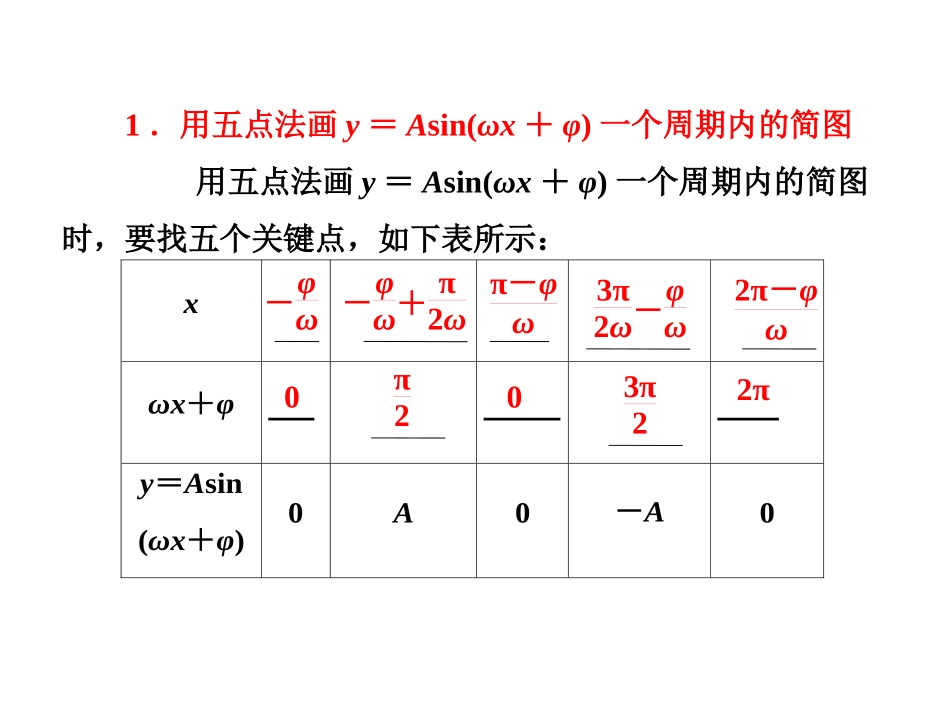
第四节正弦型函数的图象及简单应用一、课标要求1.了解函数y＝Asin(ωx＋φ)的物理意义；能画出y＝Asin(ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响．2.了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题.1．用五点法画y＝Asin(ωx＋φ)一个周期内的简图用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示：xωx＋φy＝Asin(ωx＋φ)0A0－A0－φω－φω＋π2ωπ－φω3π2ω－φω2π－φω0π203π22π2．函数y＝sinx的图象变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的步骤法一法二3．y＝Asin(ωx＋φ)的有关概念振幅周期频率相位初相y＝Asin(ωx＋φ)(A＞0，ω＞0)，x∈[0，＋∞)表示一个振动量时AT＝f＝1T＝ω2πφ2πωωx＋φ[探究]1.用五点法作y＝Asin(ωx＋φ)的图象，应先确定哪些数据？提示：先确定ωx＋φ，即先使ωx＋φ等于0，π2，π，3π2，2π，然后求出x的值．[探究]2.在图象变换时运用“先平移后伸缩”与“先伸缩后平移”两种途径，向左或向右平移的单位个数为什么不一样？提示：可以看出，前者平移|φ|个单位，后者平移φω个单位，原因在于相位变换和周期变换都是针对变量x而言的，因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序，否则会出现错误．牛刀小试1．y＝2sin2x－π4的振幅、频率和初相分别为()A．2，1π，－π4B．2，12π，－π4C．2，1π，－π8D．2，12π，－π82．函数y＝cosx(x∈R)的图象向左平移π2个单位长度后，得到函数y＝g(x)的图象，则g(x)的解析式应为g(x)＝()A．－sinxB．sinxC．－cosxD．cosx3．将函数y＝sin2x＋π6的图象向右平移π4个单位长度后得到的函数图象的对称轴是()A．x＝kπ2＋5π6，k∈ZB．x＝kπ2＋5π12，k∈ZC．x＝kπ2－π6，k∈ZD．x＝kπ－π12，k∈Z4．已知函数f(x)＝sin(ωx＋φ)(ω＞0)的图象如图所示，则ω＝________.5．把y＝sin12x的图象上点的横坐标变为原来的2倍(纵坐标不变)得到y＝sinωx的图象，则ω的值为________．例1.已知函数y＝2sin2x＋π3，(1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；(3)说明y＝2sin2x＋π3的图象可由y＝sinx的图象经过怎样的变换而得到．解(1)y＝2sin2x＋π3的振幅A＝2，周期T＝2π2＝π，初相φ＝π3.（2)令X＝2x＋π3，则y＝2sin2x＋π3＝2sinX.列表，并描点画出图象：x－π6π12π37π125π6X0π2π3π22πy＝sinX010－10y＝2sin2x＋π3020－203)方法一把y＝sinx的图象上所有的点向左平移π3个单位，得到y＝sinx＋π3的图象，再把y＝sinx＋π3的图象上的点的横坐标缩短到原来的12倍(纵坐标不变)，得到y＝sin2x＋π3的图象，最后把y＝sin2x＋π3上所有点的纵坐标伸长到原来的2倍(横坐标不变)，即可得到y＝2sin2x＋π3的图象．方法二将y＝sinx的图象上每一点的横坐标x缩短为原来的12倍，纵坐标不变，得到y＝sin2x的图象；再将y＝sin2x的图象向左平移π6个单位，得到y＝sin2x＋π6＝sin2x＋π3的图象；再将y＝sin2x＋π3的图象上每一点的横坐标保持不变，纵坐标伸长为原来的2倍，得到y＝2sin2x＋π3的图象．互动探究若将本例(3)中“y＝sinx”改为“y＝2cos2x”，则如何变换？变式训练1．为了得到函数y＝sin2x－π3的图象，只需把函数y＝sin2x＋π6的图象()A．向左平移π4个单位长度B．向右平移π4个单位长度C．向左平移π2个单位长度D．向右平移π2个单位长度2．把函数y＝sin(ωx＋φ)(ω＞0，|φ|＜π)的图象向左平移π6个单位长度，再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象表示的函数解析式为y＝sinx，则ω＝________，φ＝________.[例2](1)(2013·四川高考)函数f(x)＝2sin(ωx＋φ)ω＞0，－π2＜φ＜π2的部分图象如图所示，则ω，φ的值分别是()A．2，－π3B．2，－π6C．4，－π6D．4，π3(2)已知函数...