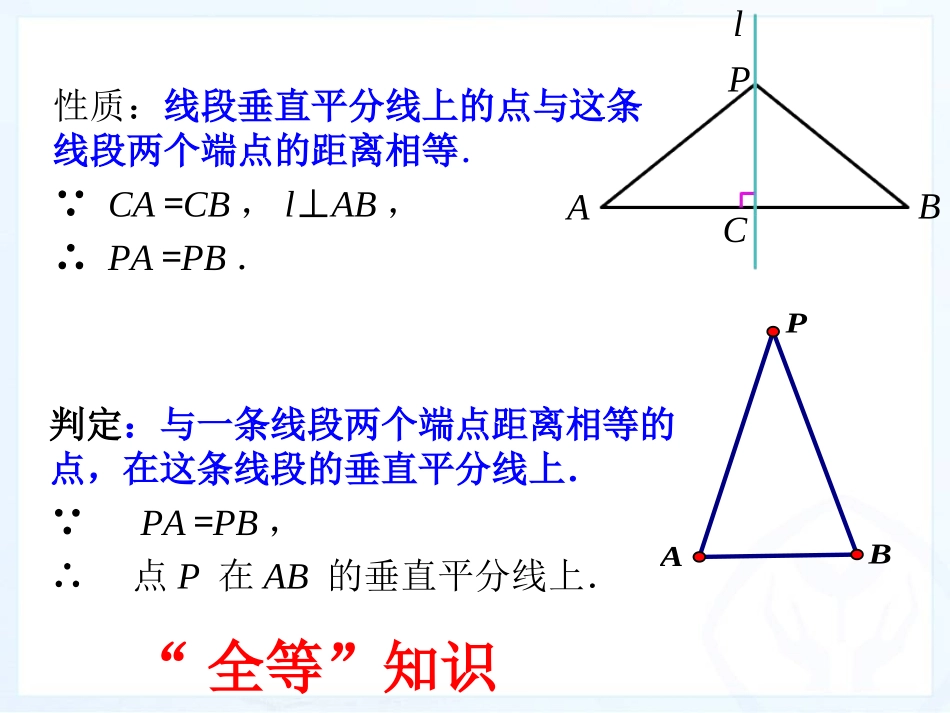
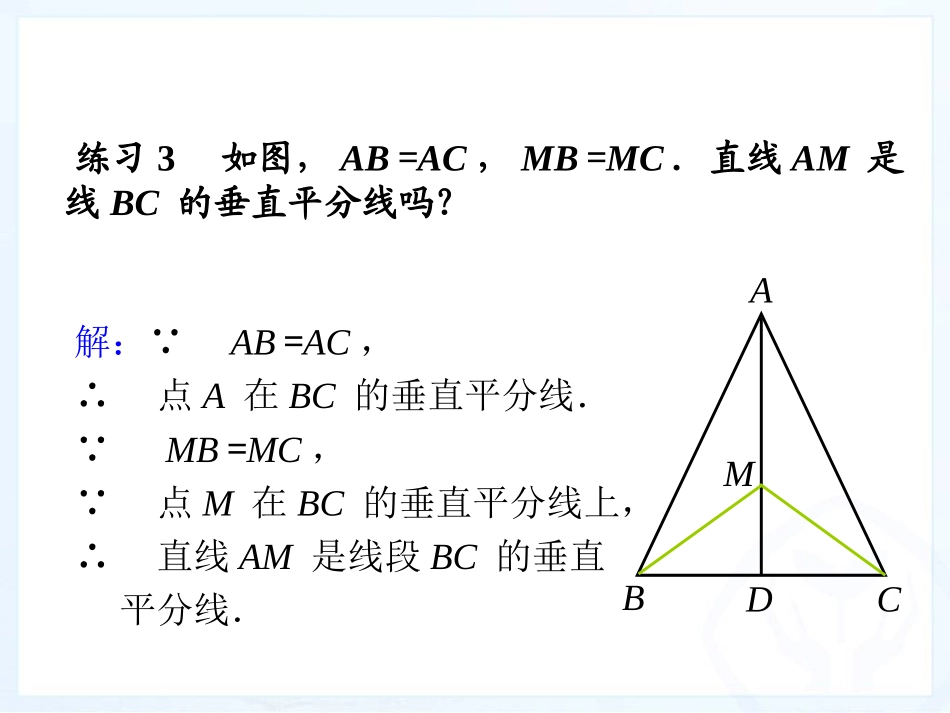
13.1轴对称(第3课时)性质:线段垂直平分线上的点与这条线段两个端点的距离相等.∵CA=CB,l⊥AB,∴PA=PB.ABPCl判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.∵PA=PB,∴点P在AB的垂直平分线上.ABP“全等”知识解:∵AB=AC,∴点A在BC的垂直平分线.∵MB=MC,∵点M在BC的垂直平分线上,∴直线AM是线段BC的垂直平分线.练习3如图,AB=AC,MB=MC.直线AM是线BC的垂直平分线吗?ABCDM如图所示,已知等腰三角形ABC,AB边的垂直平分线交AC于D,AB=AC=8,BC=6,求△BDC周长.图1-3-4如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在()的垂直平分线上.A.ABB.ACC.BCD.不能确定图1-3-31.如图,下列说法正确的是()A.若AC=BC,则CD是线段的垂直平分线;B.若AD=DB,则AC=BCC.若CD⊥AB,则AC=BC;D.若CD是线段AB的垂直平分线,则AC=BC图1-3-1(1)为什么任意取一点K,使点K与点C在直线两旁?尺规作图如何用尺规作图的方法经过直线外一点作已知直线的垂线?12DE(2)为什么要以大于的长为半径作弧?(3)为什么直线CF就是所求作的垂线?CABDKFE作线段的垂直平分线例1如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?AB这种作法的依据是什么?这种作图方法还有哪些作用?确定线段的中点.作法:如图.(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧相交于C,D两点;(2)作直线CD.CD就是所求作的直线.12作线段的垂直平分线怎样作线段AB的垂直平分线呢?ABCD作轴对称图形的对称轴如果两个图形成轴对称,怎样作出图形的对称轴?如果两个图形成轴对称,其对称轴是任何一对对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.作轴对称图形的对称轴如图中的五角星,请作出它的一条对称轴.五角星的对称轴有什么特点?作轴对称图形的对称轴你能作出这个五角星的其他对称轴吗?它共有几条对称轴?相交于一点.完成书上练习课堂练习练习2如图,角是轴对称图形吗?如果是,它的对称轴是什么?课堂练习练习3如图,与图形A成轴对称的是哪个图形?画出它的对称轴.ABCD(1)本节课学习了哪些内容?(2)作线段的垂直平分线的依据是什么?举例说明这种作法有哪些运用?(3)如何用尺规作轴对称图形的对称轴?课堂小结(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作一个角的平分线;(4)经过已知直线外一点作这条直线的垂线.(5)作一条线段的垂直平分线。作线段的垂直平分线我们已能用尺规完成:教科书习题13.1第10、12题.布置作业