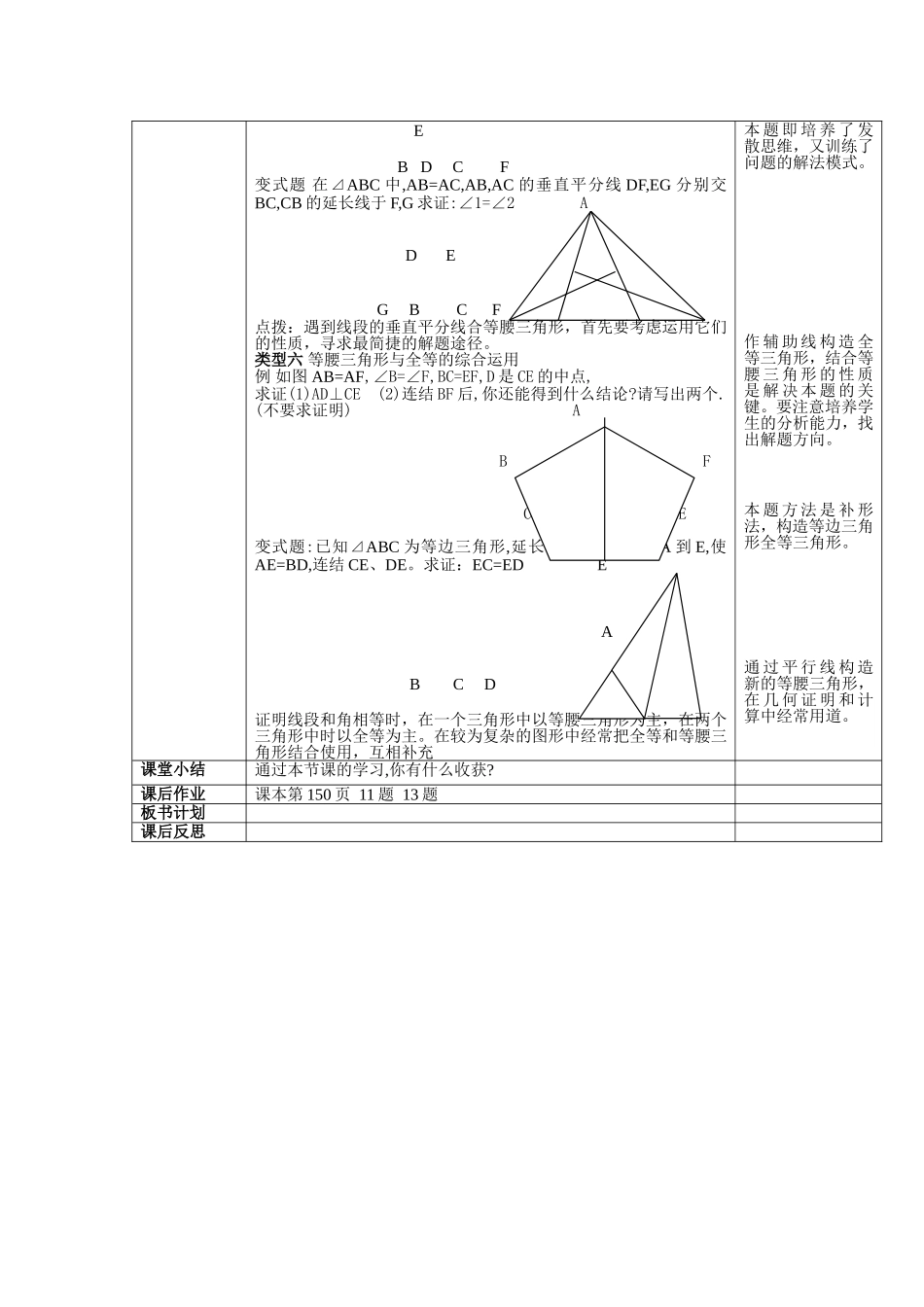
等腰三角形习题课教学设计摘要:本节课是等腰三角形复习课,以学生动手实践、自主探究、合作交流为主,培养学生动手实践能力、探索创新能力和用数学思考与解决问题能力关键词:等腰三角形、中垂线、全等教材分析:1、教材的地位和作用:等腰三角形是人教试验版八年级第十二章第三单元的知识。本节课是在学习了全等三角形、轴对称、等腰三角形之后的一节复习课。它即是对本单元知识的深化和运用,有能使学生对各部分知识的整合形成良好的体系。从纷繁复杂的题型中整理出清晰的思路。对培养学生观察,分析,归纳的能力具有深远的意义。2、教学目标知识与技能:掌握等腰三角形的性质与判定,结合全等,线段的中垂线,角的平分线进行有关计算与证明。培养观察,分析,归纳的能力。过程与方法:经历观察,分析,探究的学习过程,发展学生的思维体系。培养学生勤于思考的优秀的学习品质。情感态度价值观:通过引导学生对图形观察,发现,激发学生的求知欲。并在运用数学知识解决问题的活动中体验成功的喜悦,建立学好数学的信心。3、教学重点与难点重点:等腰三角形的性质与判定难点:结合等腰三角形,全等,中垂线进行计算和证明学情分析:学生在学习了等腰三角形以后,几经掌握了它的性质和判定。但在与其他知识的整合中还存在思路不清晰、计算和证明有困难的问题。教学策略:1、计算机辅助教学2、讨论式教学3教法:采用“情境—问题—探究—反思—提高”,使学生初步体验到数学是一个充满着观察、实验、归纳、类比和猜测的探索过程。教学过程设计:教学环节教学内容与方法师生活动与设计意图一、设置疑问导入新课学习了等腰三角形以后,你在解决问题的时候,有哪些疑惑教师提问,学生回答,同学之间互评,补充。建立和谐的课堂气氛。二.知识的分类与整合类型一:运动等腰三角形的性质进行有关的计算例:如图:在ABC中,AB=AC,AD=BD,AC=CD。求:∠B的度数。ABDC让学生观察、分析、发现、探究,找出解题方向,培养学生分析能力,建立思维体系。通过已知条件找到等角,再运用外角、内角和的相关知识,建立方程求变式题:如图,在ABC中,AB=AC,BD=BC,AD=DE=BE,求∠A的度数。ADEBC通过已知条件找到等角,再运用外角、内角和的相关知识,建立方程求解类型二运用于等腰三角形性质证明有关结论A例如图,AB=AC,BD=CD,求证:AE⊥BCDBC变式题:如图:已知∠AOB是一建筑钢架,∠AOB=12°为了使钢架更加稳固,需在内部添加一些钢条CD、DE、EF……并且钢条的长度都与OE相等。问最多能添加这样的钢条多少根?GIEOFH类型三运用等腰三角形的判定证明有关结论A以知:在⊿ABC中∠BAC=90°,AD⊥BC于DBF平分∠ABC求证:AE=AFEFBDC类型四等腰三角形的性质与判定的综合应用例在RTABC中,∠CBA=90°BF=FC,求证AF=DFAFEBCD变式题⊿ABC是等边三角形,且DE⊥BC,DF⊥AB,EF⊥AC.则⊿DEF是等边三角形,为什么?AEFBDC类型五等腰三角形与线段的垂直平分线的综合运用例如图,AD平分∠BAC,EF垂直平分AD,求证:∠B=∠CAFA解。证明线段的垂直,可以用三角形全等的方法,但很麻烦。借助等腰三角形的性质很方便,这是证明垂直问题的又一个重要的思路和方法。灵活运用等腰三角形的性质可以使计算和证明简单明确。运用等腰三角形的性质解决生活中实际问题培养学生应用数学知识解决问题的能力,获取成功的体验,提高学习数学的兴趣和自信心。等腰三角形的性质及判定经常在同一道题中出现,要熟练掌握。EBDCF变式题在⊿ABC中,AB=AC,AB,AC的垂直平分线DF,EG分别交BC,CB的延长线于F,G求证:∠1=∠2ADEGBCF点拨:遇到线段的垂直平分线合等腰三角形,首先要考虑运用它们的性质,寻求最简捷的解题途径。类型六等腰三角形与全等的综合运用例如图AB=AF,∠B=∠F,BC=EF,D是CE的中点,求证(1)AD⊥CE(2)连结BF后,你还能得到什么结论?请写出两个.(不要求证明)ABFCED变式题:已知⊿ABC为等边三角形,延长BC到D,延长BA到E,使AE=BD,连结CE、DE。求证:EC=EDEABCD证明线段和角相等时,在一个三角形中以等腰三角形为主,在两个三角形中时以全等为主。在较为复杂的图形中经常把全等和等腰三角形结合使用,互相补充本题即培养了发散思维,又训练了问题的解...