平行线分线段成比例.VIP免费

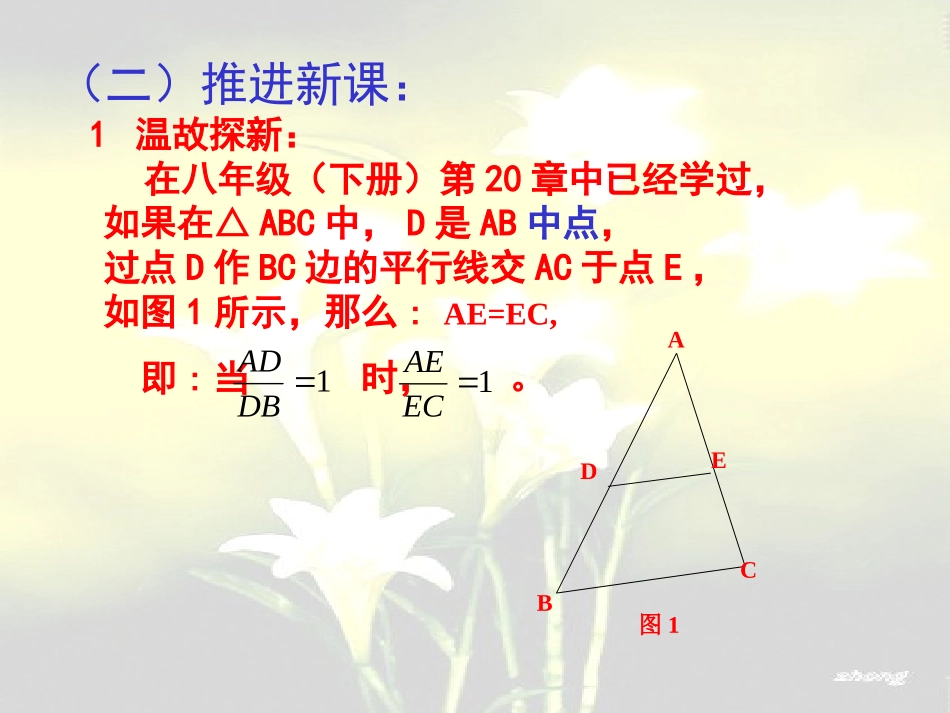
23.1.3平行线分线段成比例(1)授课人：杜奇志授课时间：2011.10.20————平行于三角形一边的直线的性质（一）复习引入：1.求出下列各式中的x:y.①3x=5y;x=;②x:y=5:3x:y=2:32.已知X:Y=7:2,求X:(X+Y).X:(X+Y)=7:93.已知X:2=Y:3=z:4，求（X+Y+Z）：（2X+3Y-Z）9k:9k=1y32（二）推进新课：1温故探新：在八年级（下册）第20章中已经学过，如果在△ABC中，D是AB中点，过点D作BC边的平行线交AC于点E，如图1所示，那么:AE=EC,即:当时，。1DBADABCDE图11ECAE如果再取AD中点G，过G点作GH∥DE交AC于点H,如图2所示，由上可得：,.31GBAG31HCAH,ADEBCGH图2上面的例子告诉我们，在△ABC的边AB上，取特殊点GD,过它们作直线平行于BC，并分别交AC于点HE时，则有：，ECAEDBADHCAHGBAG2逐步探究：平行于三角形一边的直线的性质例题：已知：如图3所示，过△ABC上任意一点D作直线DE平行于BC交AC于点E。求证：ECAEDBADADEBC图3于是我们有理由猜想：当D为AB上任意一点时，上述性质是否仍然成立呢？下面请看：证明：如图4所示，连接BE,CD,过点E作AB上的垂线段h.ADEBCh图4hSAD21ADE△∵，hSBDB21DE△SSBDEADE△△hDBh21AD21DBAD∴=SSCEDADE△△ECAE同理可得：又∵DE∥BC∴SCED△△SBDESSBDEADE△△SSCEDADE△△∴DBADECAE∴=⑴上面的比例式成立，则由例1可知，下面的比例式也随之成立：ABADACAEDBABECAC=,=.ADEBCh图4DBAD=ECAE∴下上()下上全上()全上下全()下全（2）思考探究1：如果直线DE分别交ABAC的延长线于点DE,能否得到类似如下结论呢？如果能，请给出证明。DBAD=ECAEABCDE图5.1ABCDEh图5.2→（3）思考探究2：如果直线DE分别交ABAC的反向延长线于点DE,能否得到类似如下结论呢？如果能，请给出证明。DBAD=ECAECBADED’E’图6.2CBADE图6.1类似于→→ADEBCh图4ADEBC图3（4）思考探究3：图3的图形，也可看作是直线BC平行于△ADE的一边与它的另两边延长线而得到。ADEBCh→于是得到如下定理：定理：平行于三角形一边的直线截其他两边（或两边延长线），所得对应线段成比例。（思考：能否将此定理推广成一般形式）ADEBC甲CBADE丙ABCDE乙（三）知识运用：1.如图7所示，已知：点BD在∠A的一条边上，点CE在∠A的另一条边上，且DEBC.∥若AB=14,AC=18,AE=11.求：AD的长。2.如图8所示，当点BC在∠BAC的两边上，点DE在∠BAC的两边的反向延长线上，且DEBC∥。若AB=5,AC=6,AD=2.求：AE的长。ACEDB图7EDABC图8（四）课堂小结：1.本节课你学到了什么？平行于三角形一边的直线的性质（三种具体情形）①该直线与三角形另外两边相交；②该直线与三角形另外两边的延长线相交；③该直线与三角形另外两边的反向延长线相交；2.本节课的重点和难点是？（理解推理过程，学会运用定理)（对应线段的确认）小结小结（五）作业布置：①课堂作业：教材第68页习题23.1第34题。②家庭作业：完成习题23.1相应部分，以及基础训练23.1基础平台三四。谢谢大家！谢谢大家！小结小结