必修4《三角函数的图像》讲课课件VIP免费

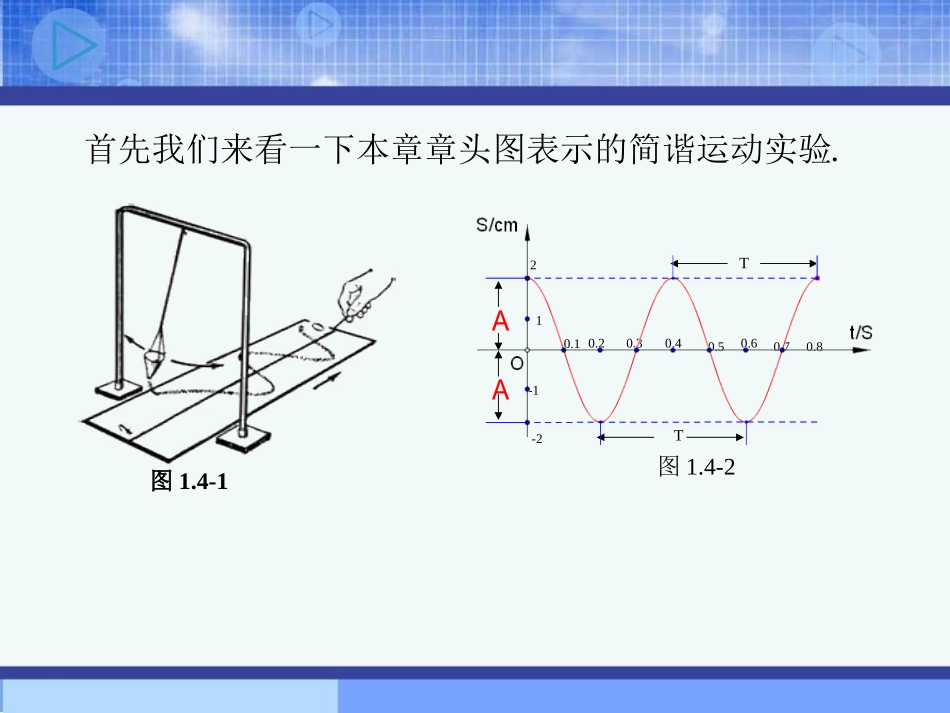
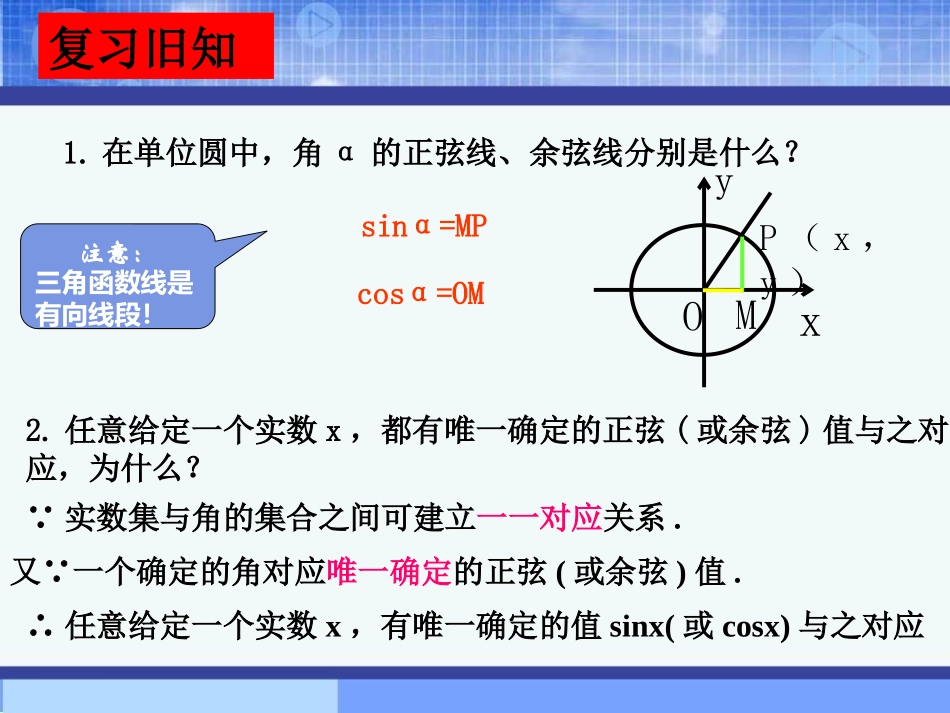
图1.4-1图1.4-2AA-1-2120.10.20.30.40.50.60.70.8TT.首先我们来看一下本章章头图表示的简谐运动实验P（x，y）OxyMsinα=MPcosα=OM1.在单位圆中，角α的正弦线、余弦线分别是什么？复习旧知注意：三角函数线是有向线段！2.任意给定一个实数x，都有唯一确定的正弦(或余弦)值与之对应，为什么？∵实数集与角的集合之间可建立一一对应关系.又∵一个确定的角对应唯一确定的正弦(或余弦)值.∴任意给定一个实数x，有唯一确定的值sinx(或cosx)与之对应我们把由这个对应法则所确定的函数y=sinx叫做正弦函数y=cosx叫做余弦函数问：这两个函数的定义域是什么？3.我们知道，任意给定一个实数x，有唯一确定的值sinx(或cosx)与之对应.定义域都是R遇到一个新函数画出函数图象，观察图象研究性质:值域、单调性、奇偶性、最值等(1)列表(2)描点(3)连线632326567342335611202123012123212300212312,0,sinxxy回顾：用描点法作出函数图象的主要步骤是怎样的？---223xy0211---xy正弦函数的图象如何在直角坐标系中比较精确地描出这些点，并画出y=sinx在[0，2π]内的图象？下面介绍一种新画法：几何画法用单位圆中正弦线表示正弦的方法,如何作出点？)6sin6(，)6sin6(，O1OyXAPM622函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法:(1)等分3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2正弦曲线xy---------1-12o46246y=sinxx[0,2]y=sinxxRyxo1-122322思考：我们在作正弦函数y=sinxx[0,2∈π]的图象时，描出了12个点，但其中起关键作用的点是哪些？分别说出它们的坐标。(0,0)(,1)2(,0)(,-1)23(2,0)五个关键点—(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)xsinx22302010-10五点画图法x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同你能确定关键的五点吗？关系？【正弦函数、余弦函数的图象】思考：能否利用正弦函数的图象向右平移得到余弦函数的图象？y=cosx=sin(x-),xR2？？例1．画出下列函数的简图（1）y=sinx+1,x∈[0,2π]列表描点作图-2223211-xyo-xxsin1sinx101010210102232（2）y=－cosx,x∈[0,2π]解:（1）]2,0[,sin1xxy]2,0[,sinxxy2-22311xyo-（2）xxcosxcos0223210-101-1010-1]2,0[,cosxxy]2,0[,cosxxy例2当x∈[0，2π]时，求不等式的解集.1cos2x³5[0,][,2]33xyO2ππ122-112y拓展练习：1作出函数y＝1－cos2x的图象．【解】y＝1－cos2x＝|sinx|.先作出y＝sinx的图象，如图1；再把x轴下方部分沿x轴翻折上来，即可得到y＝|sinx|的图象，如图2.作出函数y＝sinx＋32π在x∈[－2π，2π]上的图象．21作出函数y＝sinx＋32π在x∈[－2π，2π]上的图象．解：由于y＝sinx＋3π2＝|cosx|，因此只需作出函数y＝|cosx|，x∈[－2π，2π]的图象即可．2小结：1.正弦曲线、余弦曲线几何画法五点法(画简图)2.注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]其中五点法最常用，要牢记五个关键点的坐标。课后练习：（1）作函数y=1+3cosx，x[0,2π]∈的简图(２)作函数y=2sinx-1，x[0,2π]∈的简图（1）yx作业：课本、导学练习