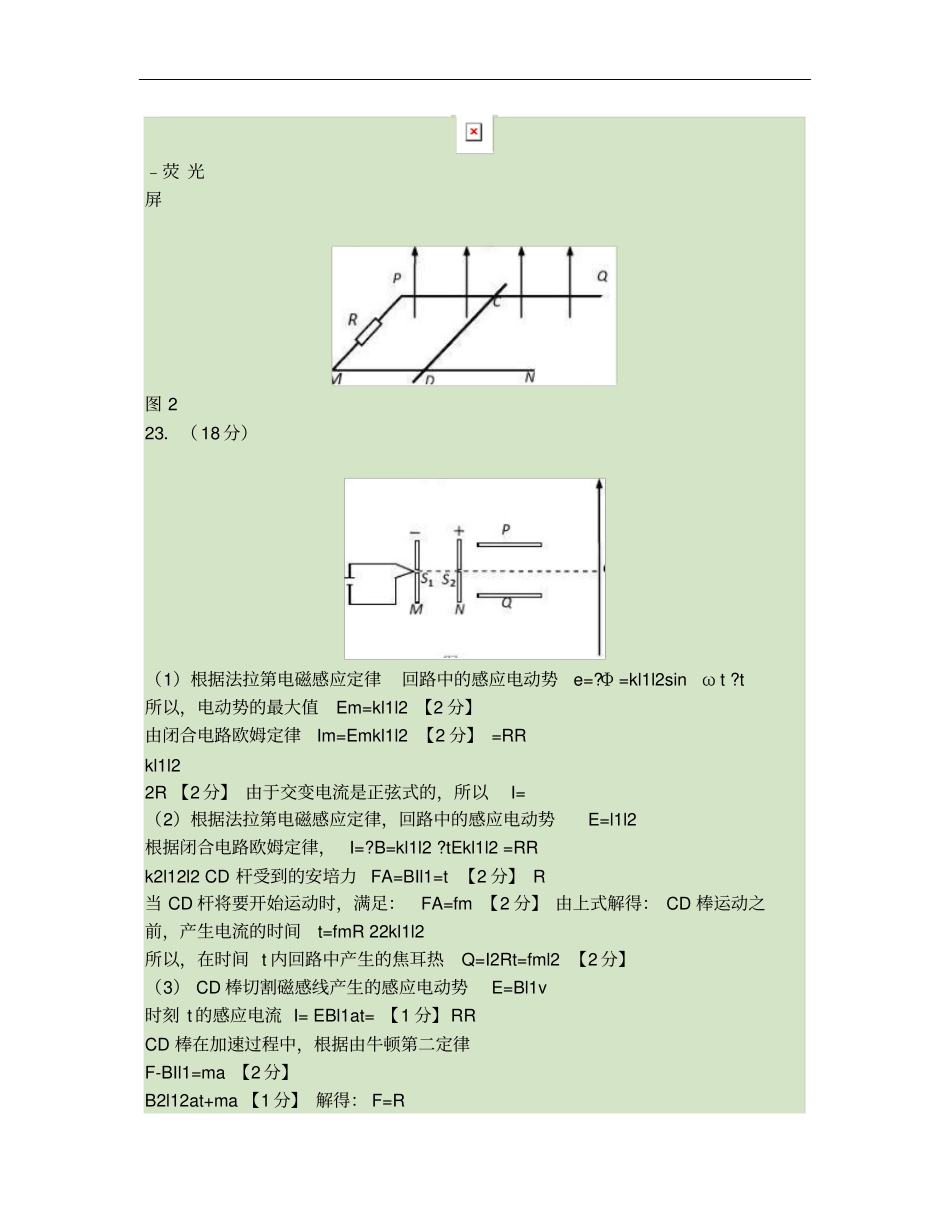
磁场电磁感应23(18分)如图1所示,两根间距为l1的平行导轨PQ和MN处于同一水平面内,左端连接一阻值为R的电阻,导轨平面处于竖直向上的匀强磁场中。一质量为m、横截面为正方形的导体棒CD垂直于导轨放置,棒到导轨左端PM的距离为l2,导体棒与导轨接触良好,不计导轨和导体棒的电阻。(1)若CD棒固定,已知磁感应强度B的变化率?B随时间t的变化关系式为?t?B=ksinωt,求回路中感应电流的有效值I;?t(2)若CD棒不固定,棒与导轨间最大静摩擦力为fm,磁感应强度B随时间t变化的关系式为B=kt。求从t=0到CD棒刚要运动,电阻R上产生的焦耳热Q;(3)若CD棒不固定,不计CD棒与导轨间的摩擦;磁场不随时间变化,磁感应强度为B。现对CD棒施加水平向右的外力F,使CD棒由静止开始向右以加速度a做匀加速直线运动。请在图2中定性画出外力F随时间t变化的图象,并求经过时间t0,外力F的冲量大小I。F图1O图224(20分)如图1所示,M、N为竖直放置的平行金属板,两板间所加电压为U0,S1、S2为板上正对的小孔。金属板P和Q水平放置在N板右侧,关于小孔S1、S2所在直线对称,两板的长度和两板间的距离均为l;距金属板P和Q右边缘l处有一荧光屏,荧光屏垂直于金属板P和Q;取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴。M板左侧电子枪发射出的电子经小孔S1进入M、N两板间。电子的质量为m,电荷量为e,初速度可以忽略。不计电子重力和电子之间的相互作用。(1)求电子到达小孔S2时的速度大小v;(2)若板P、Q间只存在垂直于纸面向外的匀强磁场,电子刚好经过P板的右边缘后,打在荧光屏上。求磁场的磁感应强度大小B和电子打在荧光屏上的位置坐标x;(3)若金属板P和Q间只存在电场,P、Q两板间电压u随时间t的变化关系如图2所示,单位时间内从小孔S1进入的电子个数为N。电子打在荧光屏上形成一条亮线。忽略电场变化产生的磁场;可以认为每个电子在板P和Q间运动过程中,两板间的电压恒定。a.试分析在一个周期(即2t0时间)内单位长度亮线上的电子个数是否相同。b.若在一个周期内单位长度亮线上的电子个数相同,求2t0时间内打到单位长度亮线上的电子个数n;若不相同,试通过计算说明电子在荧光屏上的分布规律。﹣荧光屏图223.(18分)(1)根据法拉第电磁感应定律回路中的感应电动势e=?Φ=kl1l2sinωt?t所以,电动势的最大值Em=kl1l2【2分】由闭合电路欧姆定律Im=Emkl1l2【2分】=RRkl1l22R【2分】由于交变电流是正弦式的,所以I=(2)根据法拉第电磁感应定律,回路中的感应电动势E=l1l2根据闭合电路欧姆定律,I=?B=kl1l2?tEkl1l2=RRk2l12l2CD杆受到的安培力FA=BIl1=t【2分】R当CD杆将要开始运动时,满足:FA=fm【2分】由上式解得:CD棒运动之前,产生电流的时间t=fmR22kl1l2所以,在时间t内回路中产生的焦耳热Q=I2Rt=fml2【2分】(3)CD棒切割磁感线产生的感应电动势E=Bl1v时刻t的感应电流I=EBl1at=【1分】RRCD棒在加速过程中,根据由牛顿第二定律F-BIl1=ma【2分】B2l12at+ma【1分】解得:F=RF根据上式可得到外力Ft0,外力F的冲量I?1?B2l12aI=?(t0+ma)+ma?t02?R?2B2l12at0+mat0【2分】解得:I=2R24.(20分)(1)根据动能定理1eU0=mv2【3分】2解得:v=2eU0①【3分】m(2)电子在磁场中做匀速圆周运动,设圆运动半径为R,在磁场中运动轨迹如图,由几何关系lR2=l2+(R-)225解得:R=l【2分】4v2根据牛顿第二定律:Bev=m【1分】R42mU0解得:B=【1分】5lel4设圆弧所对圆心为α,满足:sinα==R5由此可知:tanα=xO43x-电子离开磁场后做匀速运动,满足几何关系:通过上式解得坐标x=ll=tanα【1分】11l6【1分】(3)a.设电子在偏转电场PQ中的运动时间为t1,PQ间的电压为u垂直电场方向:l=vt1②12at1③2eu此过程中电子的加速度大小a=④ml平行电场方向:x1=ul①、②、③、④联立得:x1=【1分】4U0电子出偏转电场时,在x方向的速度vx=at1⑤电子在偏转电场外做匀速直线运动,设经时间t2到达荧光屏。则水平方向:l=vt2⑥竖直方向:x2=vxt2⑦①、⑤、⑥、⑦联立,解得:x2=ul【1分】2U0电子打在荧光屏上的位置坐标x=x1+x2=3lu⑧【1分】4U0对于有电子穿过P、Q间的时间内进行讨论:由图2可知,在任意?t时间内,P、Q间电压变...