14.2.2-完全平方公式-.VIP免费

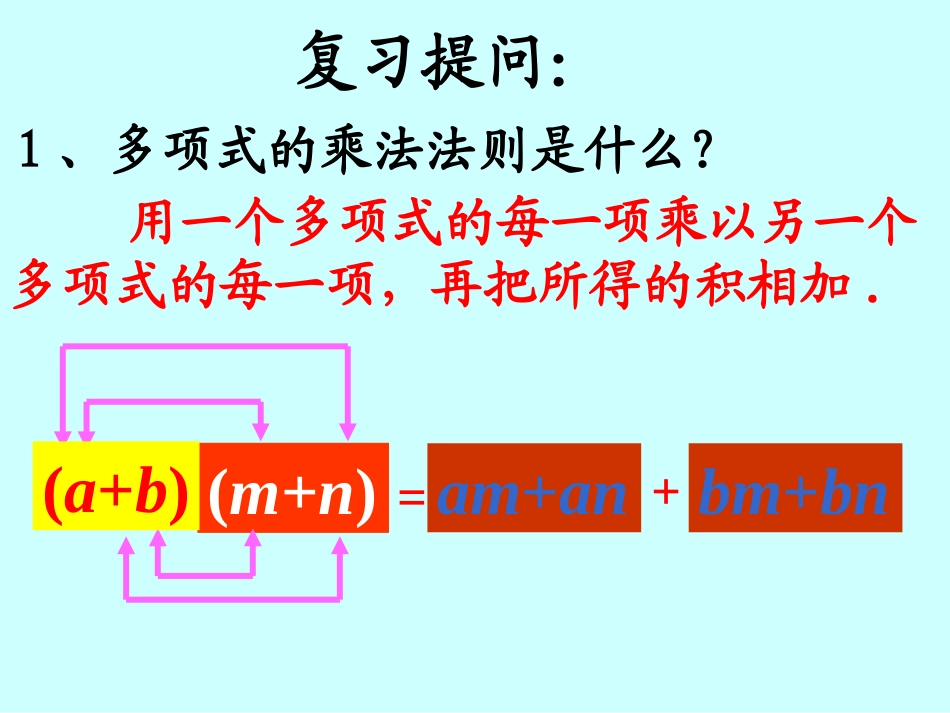
标题标题标题14.2.214.2.2完全平方公完全平方公式式叶爱华叶爱华复习提问：用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加.1、多项式的乘法法则是什么？am+anbm+bn+=(m+n)(a+b)2.平方差公式((aa++bb)()(aa−−bb))==aa22−−bb22两数和与这两数差的积两数和与这两数差的积,,等于这两等于这两数的平方的差数的平方的差..用式子表示，即：用式子表示，即：(4)(m－2)2=__________(3)(p-1)2=(p-1)(p-1)=_________(2)(m+2)2=__________计算下列各式，你能发现什么规律？（1）（p+1）2=(p+1)(p+1)=_________p2+2p+1m2+4m+4p2－2p+1m2－4m+4算一算：(a+b)2(a-b)2=a2+2ab+b2=a2-2ab+b2=a2+ab+ab+b2=a2-ab-ab+b2=(a+b)(a+b)=(a-b)(a-b)完全平方公式的数学表达式：完全平方公式的文字叙述：两个数的和（或差）的平两个数的和（或差）的平方，等于它们的平方和，加上（或方，等于它们的平方和，加上（或减去）它们的积的减去）它们的积的22倍。倍。22222222babababababa完全平方公式：两数和（或差）的平方，等于它们的平方和，加（或减去）它们的积的2倍．即:(a±b)2=a2±2ab+b2记忆口诀：首平方，尾平方,积的2倍放中间.bbaa2)(ba(a+b)²a²2ab²2bababab2++完全平方和公式：完全平方公式的图形理解aabb(a-b)²2)(ba2aab222aabba²ababab2bb²bb完全平方差公式：完全平方公式的图形理解公式特点：4、公式中的字母a，b可以表示数，单项式和多项式。(a+b)(a+b)22=a=a22+2ab+b+2ab+b22(a(a--b)b)22=a=a22--2ab+b2ab+b221、积为二次三项式；2、积中两项为两数的平方和；3、另一项是两数积的2倍，且与乘式中间的符号相同。例1运用完全平方公式计算：解:(4m+n)2==16m2(1)(4m+n)2(a+b)(a+b)22=a=a22+2a.b+b+2a.b+b22(4m)2+2•(4m)•n+n2+8mn+n2例1运用完全平方公式计算：解：(y-)2==y2(2)(y-)2(a-b)(a-b)22=a=a22-2a.b+b-2a.b+b22y2-2•y•+()2-y+2121212141练习1：下面各式的计算是否正确？如果不正确，应当怎样改正？(1)(x+y)2=x2+y2(2)(x－y)2=x2－y2(3)(x－y)2=x2+2xy+y2(4)(x+y)2=x2+xy+y2错错错错错错错错(x+y)2=x2+2xy+y2(x－y)2=x2－2xy+y2(x-y)2=x2--2xy+y2(x+y)2=x2+22xy+y2练习练习22：：利用完全平方公式计算：利用完全平方公式计算：(1)(1)(2(2xx−−3)3)22；；(2)(2)(4(4xx++55yy))22;;(3)(3)((mnmn−−aa))22使用完全平方公式与平方差公式的使用一样使用完全平方公式与平方差公式的使用一样,,先把要计算的式子与完全平方公式对照先把要计算的式子与完全平方公式对照,,明确哪个是明确哪个是aa,,哪个是哪个是b.b.第一数第一数22xx44xx2222xx的平方的平方,,(())22−−减去减去22xx第一数第一数与第二数与第二数−−22xx33••乘积乘积的的22倍倍,,••22加上加上++第二数第二数33的平方的平方..22==−−1212xx++99;;解：解：(1)(1)(2(2xx−−3)3)22做题时要做题时要边想边写：边想边写：==33练习3：运用完全平方公式计算：（1）（x＋6）2（2）（y－5）2（3）（－2x＋5）2（4）（x－y）24332例2：运用完全平方公式计算：(1)1022解：1022=(100+2)2=10000+400+4=10404(2)992解：992=(100–1)2=10000-200+1=9801练习4：运用完全平方公式计算：(1)1042解：1042=(100+4)2=10000+800+16=10816(2)99.992解：99.992=(100–0.01)2=10000-2+0.0001=9998.0001(a+b)2与(-a-b)2相等吗？(a-b)2与(b-a)2呢？(a+b)2=a2+2ab+b2(-a-b)2=(-a)2-2(-a)b+b2=a2+2ab+b2(a-b)2=a2-2ab+b2(b-a)2=b2-2ba+a2=a2-2ab+b2(a+b)2=a2+b2呢？拓展练习下列等式是否成立下列等式是否成立??说明理由．说明理由．(1)(1)((4a4a++1)1)22=(1=(1−−4a)4a)22；；(2)(2)((4a4a−−1)1)22=(4a=(4a++1)1)22；；(3)(3)(4a(4a−−1)(11)(1−−4a)4a)＝＝(4a(4a−−1)(4a1)(4a−−1)1)＝＝(4a(4a−−1)1)22；；(4)(4)(4a(4a−−1)(1)(11−−4a)4a)＝＝(4a(4a−−1)(4a1)(4a++1).1).成立成立成立成立不成立．不成立．不成立．不成立．巩固练习:1.下列各式哪些可用完全平方公式计算(1)(2a-3b)(3b-2a)(2)(2a-3b)(-3b-2a)(3)(-2m+n)(2m+n)(4)(2m+n)(-2m-n)x2+2xy+...