13.3双曲线VIP免费

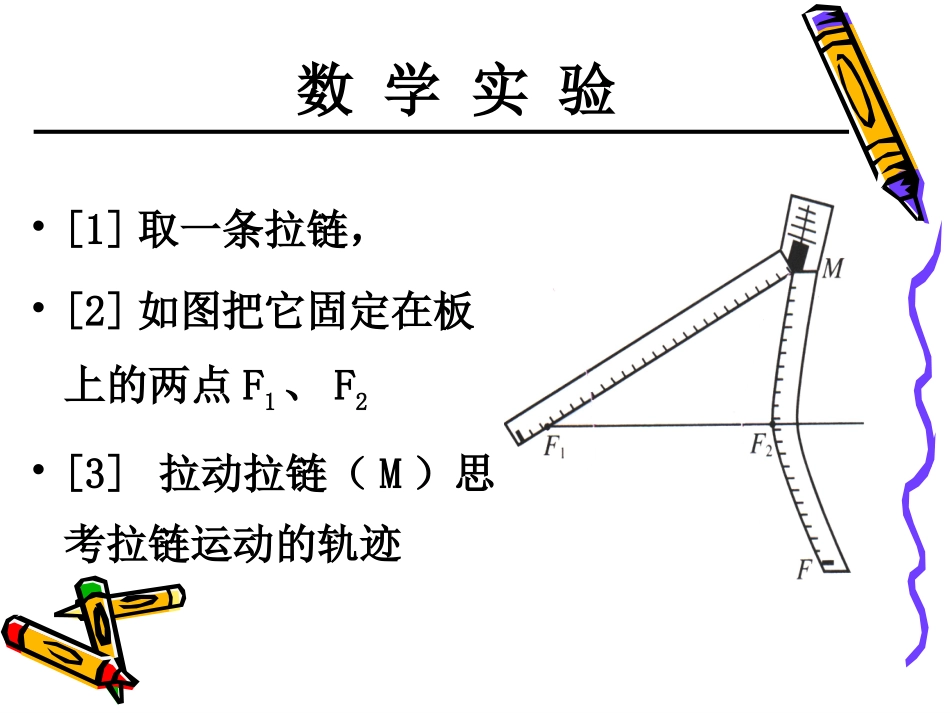
双曲线的定义及其标准方程数学实验•[1]取一条拉链，•[2]如图把它固定在板上的两点F1、F2•[3]拉动拉链（M）思考拉链运动的轨迹①①如图如图(A)(A)，，|MF|MF11||--|MF|MF22|=|=②②如图如图(B)(B)，，|MF|MF11||--|MF|MF22|=|=由①②可得：由①②可得：|||MF|MF11||--|MF|MF22||||==22aa上面两条曲线合起来叫做上面两条曲线合起来叫做双曲线双曲线,,每一条叫做每一条叫做双曲线的一支双曲线的一支..双曲线的定义22aa--22aa平面内与两定点F1，F2的距离的差的绝对值等于常数2a(小于|F1F2|)的点的轨迹叫做双曲线.MMF2F1yox..①两个定点F1、F2——双曲线的焦点.②|F1F2|=2c——焦距.没有“绝对值”这个条件时,仅表示双曲线的一支.双曲线的定义设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数为2a.以F1,F2所在的直线为x轴，线段F1F2的中点o为原点建立直角坐标系.1.建系.2.设点．3.列式．4.化简.MF2F1yox..aMFMF221aycxycx2)()(2222即双曲线的标准方程|||MF|MF11||--|MF|MF22||||==22aa222222ycxaycx)(2)(222ycxaacx)(222221xyaca得)()(22222222acayaxac0)b0,(abyax12222aycxycx2)()(22224.化简.222cab令（1）双曲线的标准方程用减号“-”连接；（2）双曲线方程中a>0,b>0,但a不一定大于b;说明：（3）如果x2的系数是正的，则焦点在x轴上；如果y2的系数是正的，则焦点在y轴上；（4）双曲线标准方程中，a，b，c的关系是c2=a2+b2.F(±c,0)12222byax12222bxayyxoF2F1MxyF2F1MF(0,±c)双曲线的标准方程判断下列方程是否表示双曲线，若是，求出三量a,b,c的值①12422yx②12222yx③12422yx④369422xy6,2,2cba2,2,2cba6,2,2cba13,2,3cba22194yx巩固练习22124yx例例11、已知双曲线两个焦点的坐标为、已知双曲线两个焦点的坐标为FF11(-5,0)(-5,0)、、FF22(5,0),(5,0),双曲线上一点双曲线上一点PP到到FF11、、FF22的距离的差的距离的差的绝对值等于的绝对值等于66，求双曲线的标准方程。，求双曲线的标准方程。解：因为双曲线的焦点在解：因为双曲线的焦点在xx轴上，所以设它的轴上，所以设它的a=3,c=5;b2=52–32=16∴所求双曲线的标准方程为221(00)22xyabab标准方程为116922yx例题讲解例2、已知双曲线的焦点为F1(-5,0),F2(5,0)双曲线上一点到焦点的距离差的绝对值等于8，则(1)a=_____,c=_____,b=_____(2)双曲线的标准方程为____________(4)双曲线上一点Ｐ，|PF1|=10,则|PF2|=_________4532或18(3)||PF1|-|PF2||=____________8221169xyPPy例题讲解ox..F1F2双曲线的双曲线的图像与性质图像与性质双曲线的双曲线的图像与性质图像与性质oyxF1F2A1A2B2B1标准方程范围对称性顶点)0(12222babyaxaxabyb对称轴：坐标轴对称中心：原点A1,A2,B1,B2(-c,0)(c,0)(a,0)(0,-b)(0,b)复习椭圆的图像与性质(-a,0)焦点在x轴上的椭圆2、对称性1、范围关于x轴、y轴和原点都对称.x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心.xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)xaxa或焦点在x轴上的双曲线的图像与性质22221(0,0)xyabab0)b0,(abyax122223、顶点xyo1B2B1A2A线段A1A2叫做双曲线的实轴，它的长为2a,a叫做双曲线的实半轴长；线段B1B2叫做双曲线的虚轴，它的长为2b,b叫做双曲线的虚半轴长.实轴与虚轴等长的双曲线叫等轴双曲线.双曲线与x轴有两个交点：A1(-a,0),A2(a,0).双曲线与y轴没有交点，但我们也把B1(0,-b),B2(0,b)画在y轴上.焦点在x轴上的双曲线的图像与性质4、渐近线1A2A1B2Bxyoxabyxabyab可以看出，双曲线的各支向外延伸时，与直线逐渐接近，我们把这两条直线叫做双曲线的渐近线.12222byaxxaby双曲线与渐近线无限接近，但永不相交.0)b0,(abyax12222焦点在x轴上的双曲线的图像与性质oxyB1B2A1A222221(0,0)yxababaayxb1.范围：2.对称性：3.顶点：4.渐近线方程：y≥a或y≤-a关于坐标轴和原点对称A1(0，-a),A2(0,a)A1A2为实轴，B1B2...