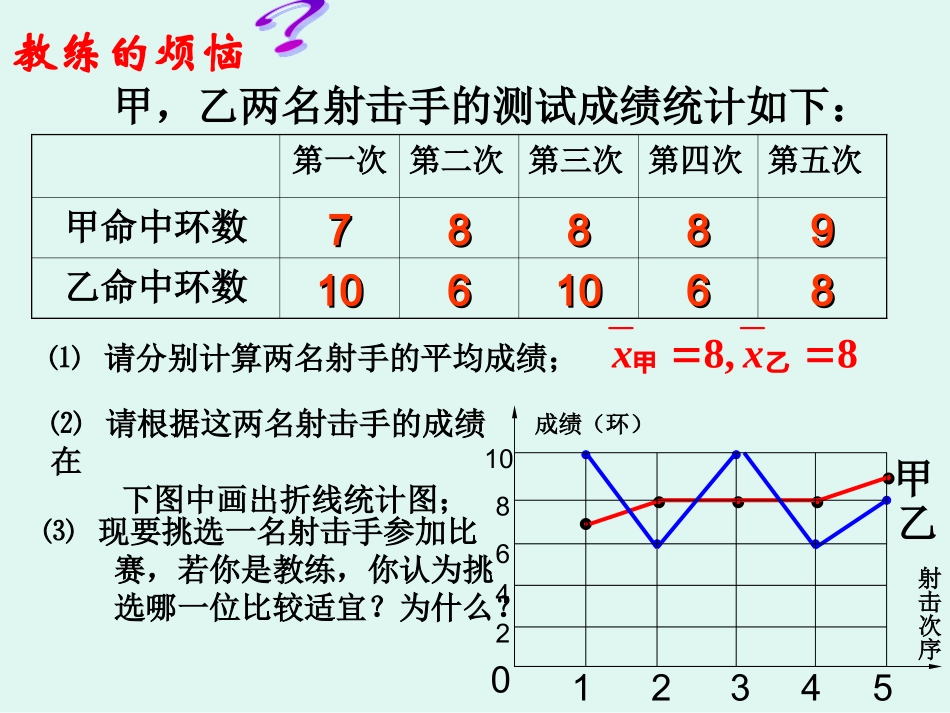
沪科版数学八年级下册20.2数据的离散程度•安徽省阜南县第一初级中学朱梅第一次第二次第三次第四次第五次甲命中环数7788888899乙命中环数10106610106688甲,乙两名射击手的测试成绩统计如下:⑴请分别计算两名射手的平均成绩;教练的烦恼甲乙⑶现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?成绩(环)射击次序012234546810⑵请根据这两名射击手的成绩在下图中画出折线统计图;8,8xx甲乙•根据计算我们可以知道甲、乙两名射击手的平均成绩都是8环,但是相比之下,甲射击手的成绩大部分都集中在8环附近,而乙射击手的成绩与其平均值的离散程度较大.通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.请同学们进一步思考,什么样的数据能反映一组数据与其平均值的离散程度?从上面的表和可以看到,甲的射击成绩与平均成绩的偏差较小,而乙的较大。那么如何说明呢?可以直接将各数据与平均值的差进行累加吗?在下表中写出你的计算结果并进行小结,可以用它们来比较两组数据围绕其平均值的波动情况(离散程度)吗?第一次第二次第三次第四次第五次求和甲射击成绩78889每次成绩与平均成绩之差乙射击成绩1061068每次成绩与平均成绩之差-1000102-22-200你的小结是什么?能用上面的方法比较两组数据的波动情况吗?•不能,每次相减的差有正有负,求和时可能同为0,或是其它的同一数字,这样就无法比较了!如果将每次的差都平方再求和,能解决上面的问题吗?试一下……此时甲求和后为2,乙求和后为16,可以解决上面的问题。那么这种方法适用于所有的情况吗?看一下下面的问题,想一想,算一算,再来给出你的结论吧!•如果一共进行了七次射击测试,而甲因故缺席了两次,怎样比较谁的成绩更稳定呢?用上面的方法计算一下填入下面的表格中,然后想一下这种方法适用吗?如果不适用,应该如何改进呢?1234567求和甲成绩7888缺席9缺席差的平方∕∕乙成绩106106879差的平方100012444401118对,有的同学已经发现了这种方法在这里看似是适用的,但仔细想来两组数据并不一样多,这样对数据多的一组来说不公平!那么应该怎样解决呢?对,咱们的同学真聪明!求平均数就可以解决了!一组数据中,各数据与它们的平均数的差的平方的平均数。方差:方差:计算公式:2222121nSxxxxxxn=…一般步骤:求平均求平均--再求差再求差--然后平方然后平方--最后再平均最后再平均说一说•注:一组数据的方差越大,说明这组数据的波动越大,离散程度越大.做一做•例1已知样本数据101,98,102,100,99,则这个样本的方差是___________。做一做•例2为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高如下:(单位:mm)甲:9,10,11,12,7,13,10,8,12,8乙:8,13,12,11,10,12,7,7,9,11•请你经过计算后回答如下问题:•(1)哪种农作物的10株苗长的比较高?•(2)哪种农作物的10株苗长的比较整齐?练一练•1、填空题•(1)如果样本方差,那么这个样本的平均数为__________.样本容量为____________。•(2)数据1,2,3,4,5的平均数为____________,方差为_________。数据-2,-1,0,1,2的方差是_________。•(3)一组数据:-2,-1,0,x,1的平均数是0,则x=_______,方差________。练一练(2)小明和小聪最近5次数学测验成绩如下:小明7684808773小聪7882798081哪位同学的数学成绩比较稳定?练一练•3、已知的平均数10,方差3,则的平均数为__________,方差为___________。谈一谈:这节课你有有哪些收获?还有哪些困惑和感悟?与大家分享一下。布置作业•1、课本第137页:第9、10题;•2、课本第132—133页信息技术应用。