17.1勾股定理3VIP免费

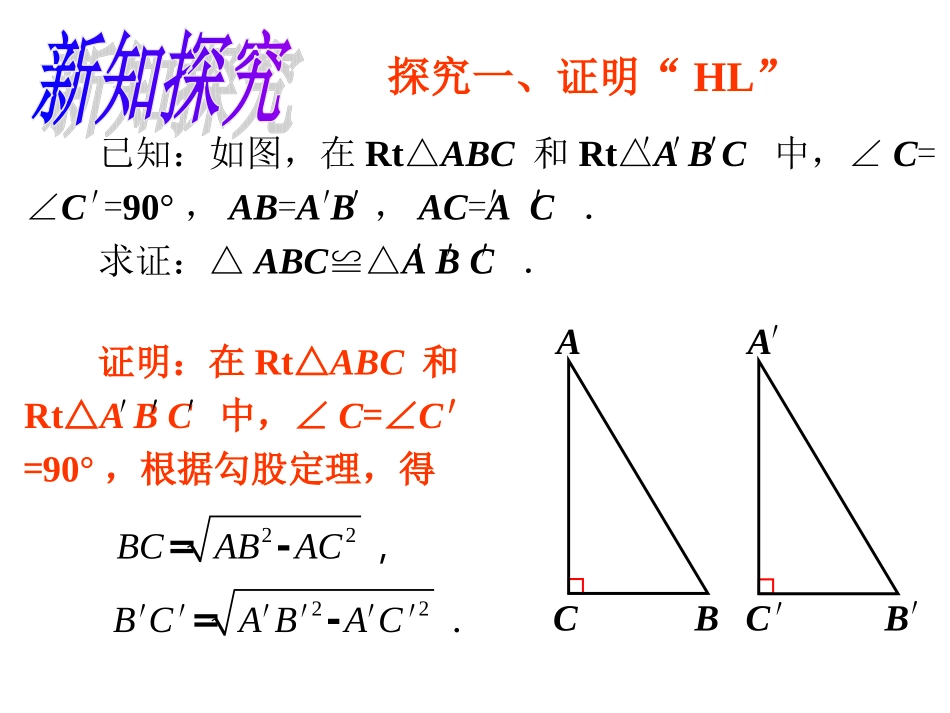
第十七章勾股定理在八年级上册中，我们曾经通过画图得到结论：斜边和一条直角边分别相等的两个直角三角形全等．学习了勾股定理后，你能证明这一结论吗？ABCABC′′′探究一、证明“HL”22=-BCABAC，22-=BCABAC．′′′′′′已知：如图，在Rt△ABC和Rt△ABC中，∠C=∠C=90°，AB=AB，AC=AC．求证：△ABC≌△ABC．′′′′′′′′′′′证明：在Rt△ABC和Rt△ABC中，∠C=∠C′=90°，根据勾股定理，得′′′ABCABC′′′ABCABC′′′′′′∴△ABC≌△ABC（SSS）．′′′′′′证明：∵AB=AB，AC=AC，∴BC=BC．你能在数轴上表示出的点吗？我们知道数轴上的点有的表示有理数，有的表示无理数2实数一一对应数轴上的点你能在数轴上画出表示的点吗？你能在数轴上画出表示的点吗？130011223344探究二、画图0011223344步骤：步骤：llAABBCC1、在数轴上找到点A,使OA=3;2、作直线lOA,⊥在l上取一点B，使AB=2;3,以原点O为圆心，以OB为半径作弧，弧与数轴交于C点，则点C即为表示的点。13数轴上的点有的表示有理数，有的表示无理数，数轴上的点有的表示有理数，有的表示无理数，你能在数轴上画出表示的点吗？你能在数轴上画出表示的点吗？13∴点C即为表示的点13试一试1、请同学们在草稿纸上再画图，在数轴上表示的点13你能在数轴上画出表示的点和你能在数轴上画出表示的点和的点吗？的点吗？1517数学海螺图：数学海螺图：利用勾股定理作出长为利用勾股定理作出长为的线段的线段..5,4,3,2,111113425400221133554411235（1）勾股定理有哪些方面的应用，本节课学习了勾股定理哪几方面的应用？（2）你能说说勾股定理求线段长的基本思路吗？（3）本节课体现出哪些数学思想方法？1.如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．求证：AD2+DB2=DE2．证明：∵∠ACB=∠ECD，∴∠ACD+∠BCD=∠ACD+∠ACE，∴∠BCD=∠ACE．又BC=AC，DC=EC，∴△ACE≌△BCD．ABCDEABCDE证明：∴∠B=∠CAE=45°，∠DAE=∠CAE+∠BAC=45°+45°=90°．∴AD2+AE2=DE2．∵AE=DB，∴AD2+DB2=DE2．例如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．求证：AD2+DB2=DE2．2.已知等边三角形ABC的边长是6cm，(1)求高AD的长；(2)S△ABCABCD解：(1)∵△ABC是等边三角形，AD是高在Rt△ABD中,根据勾股定理222BDABADcmAD3327936ADBCSABC21)2()(39336212cm321BCBD（3）求D到AB的距离ABDC变式：如图，等边△ABC，高AD=6，（1）求等边三角形的边长；（2）求△ABC的面积。3.3.如图，在四边形如图，在四边形ABCDABCD中，∠中，∠BADBAD=90=9000，∠，∠DBC=90DBC=9000，，AD=3AD=3，，AB=AB=44，，BC=12BC=12，求，求CDCD；；DABC探索勾股定理4.想一想（误差在10内为正常）我们有:好奇是人的本性!b=58a=464658cc2=a2+b2=462+582=5480而742=5476由勾股定理得：在误差范围内AB我怎么走会最近呢?5.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?(π的值取3)BA高12cmBA长18cm(π的值取3)9cm∵AB2=92+122=81+144=225=∴AB=15(cm)蚂蚁爬行的最短路程是15厘米.152