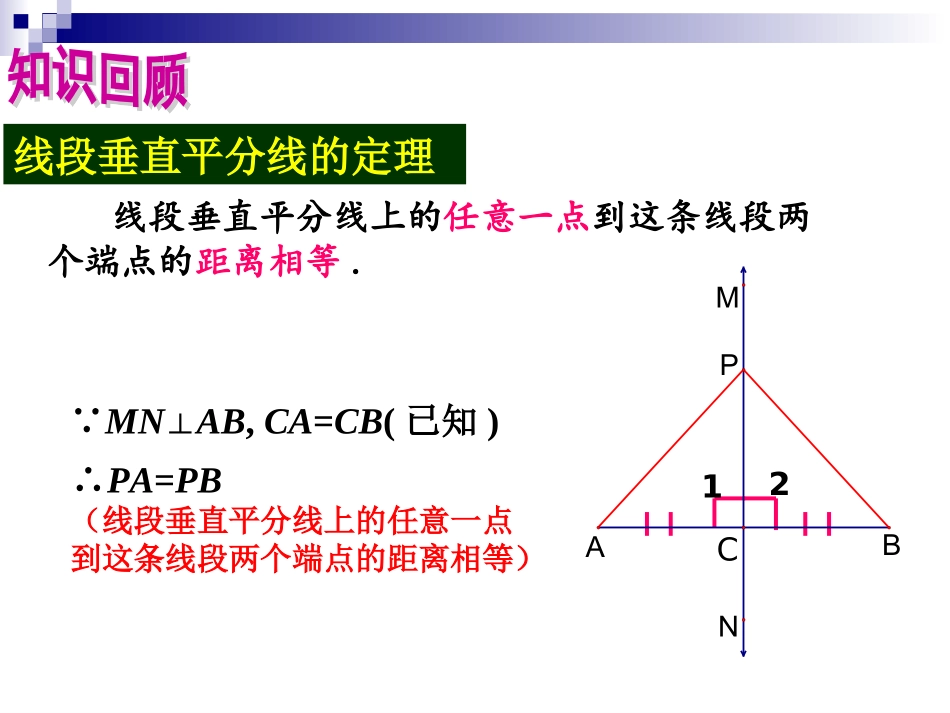
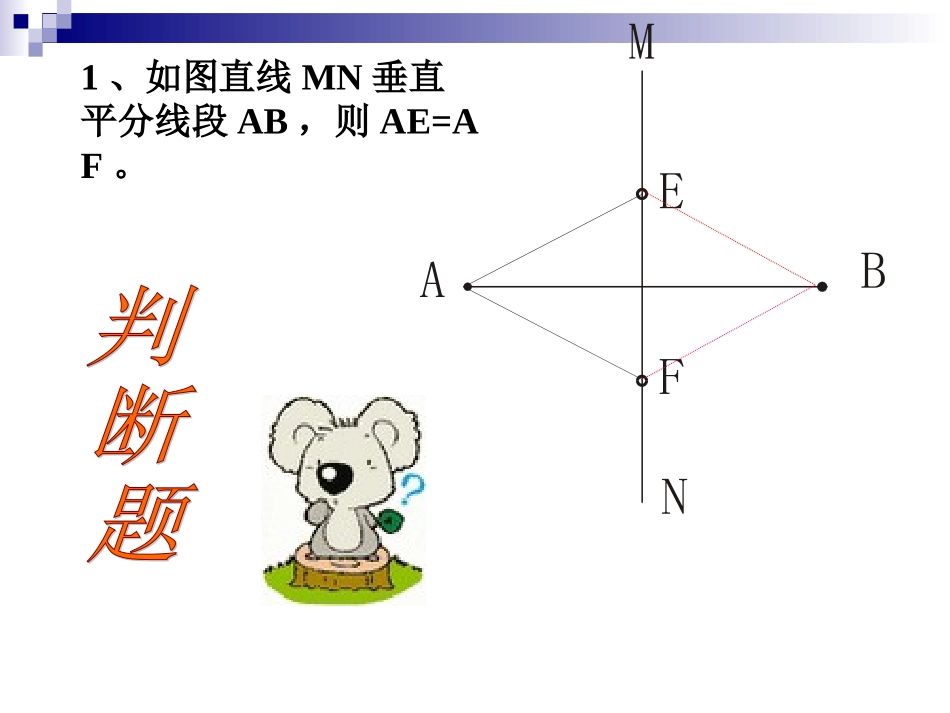
线段的垂直平分线和角平分线的复习线段的垂直平分线和角平分线的复习线段垂直平分线的定理线段垂直平分线上的任意一点到这条线段两个端点的距离相等. MN⊥AB,CA=CB(已知)∴PA=PB(线段垂直平分线上的任意一点到这条线段两个端点的距离相等)12CBAMNP1、如图直线MN垂直平分线段AB,则AE=AF。2、如图线段MN被直线AB垂直平分,则ME=NE。线段垂直平行线的逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.BCA AB=AC(已知)∴点A在线段BC的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)3、如图PA=PB,则直线MN是线段AB的垂直平分线。在角的平分线上的点到这个角两边的距离相等.角的平分线的性质定理:ABO12PEDC OP平分∠AOBPD⊥OA,PE⊥OB,∴PD=PE(在角的平分线上的点到这个角两边的距离相等).练习下列过程是否正确?ABOPED∴点P在∠AOB的平分线上. PD=PE,(在一个角的内部且到角的两边距离相等的点,在这个角的平分线上).错误. 如图,AD平分∠BAC(已知)∴=,()在角的平分线上的点到这个角的两边的距离相等。ADCBBDCD(×) 如图,DCAC⊥,DBAB⊥(已知)∴=,()在角的平分线上的点到这个角的两边的距离相等。ADCBBDCD(×)ABO12PEDC在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.角平分线性质定理的逆定理:∴OP平分∠AOB PD⊥OA,PE⊥OB,PD=PE.(在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上). AD平分∠BAC,DCAC⊥,DBAB⊥(已知)∴=,()DBDC在角的平分线上的点到这个角的两边的距离相等。ADCB√不必再证全等如图,已知及线段a,点C在OM上,求作点P,使点P到OM、ON的距离相等,且PC=a.分析:(1)到OM、ON的距离相等的点的轨迹是什么?(2)满足PC=a.点P的轨迹是什么?NMCOaP2P1∴点P1、P2为所求的点.威海市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1BAC线段的垂直平分线1、求作一点P,使它和已△ABC的三个顶点距离相等.实际问题数学化pPA=PB=PC实际问题1结论:三角形三边垂直平分线交于一点,结论:三角形三边垂直平分线交于一点,该点到三角形三个顶点的距离相等。该点到三角形三个顶点的距离相等。烟威高速公路实际问题2在烟威高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?AB线段的垂直平分线2、如图,在直线L上求作一点P,使PA=PB.LAB实际问题数学化实际问题2pPA=PB数学问题源于生活实践,反过来数学又为生活实践服务已知:如图,在等腰三角形ABC中,腰AB的垂直平线MN交AC于点D,BC=8厘米,ΔBDC的周长20厘米.求:AB的长.ABCDMN已知:如图,D是BC延长线上的一点,BD=BC+AC.求证:点C在AD的垂直平分线上.ABCD8例1已知:如图,AP、BP分别平分∠DAB和∠CBA,PE、PF分别垂直于AD、BC,垂足为E、F.求证:点P在EF的垂直平分线上.分析:(1)从已知条件你能想到什么定理?(3)能得到什么结论?(4)用什么定理来证明结论?(2)缺少了什么?怎么办?AEDPCFBG角平分线上的点到另一边的垂线段.添加辅助线.添辅助线的目的是什么?构造角平分线的基本图形.例1已知:如图,AP、BP分别平分∠DAB和∠CBA,PE、PF分别垂直于AD、BC,垂足为E、F.求证:点P在EF的垂直平分线上.证明:过点P作PG⊥AB,垂足为点G.AEDPCFBG AP平分∠BAD,PE⊥AD(已知),PG⊥AB(已作),∴PE=PG(角平分线上的点到角两边的距离相等).同理:PG=PF.∴PE=PF(等量代换).∴点P在EF的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上).例2已知:△ABC中,∠ABC角平分线与AC的垂直平分线交于点N,ND⊥AB,NE⊥BC,点D、E分别为垂足.分析:(1)从角平分线和角两边的两条垂线段,你能得到什么结论?(2)怎样来理解这个条件?CEBNAD求证:AD=EC.(3)怎样来证明结论?12点N在AC的垂直平分线上.怎样来利用这个条件?添加辅助线.添辅助线的目的是什么?构造垂直平分线的基本...