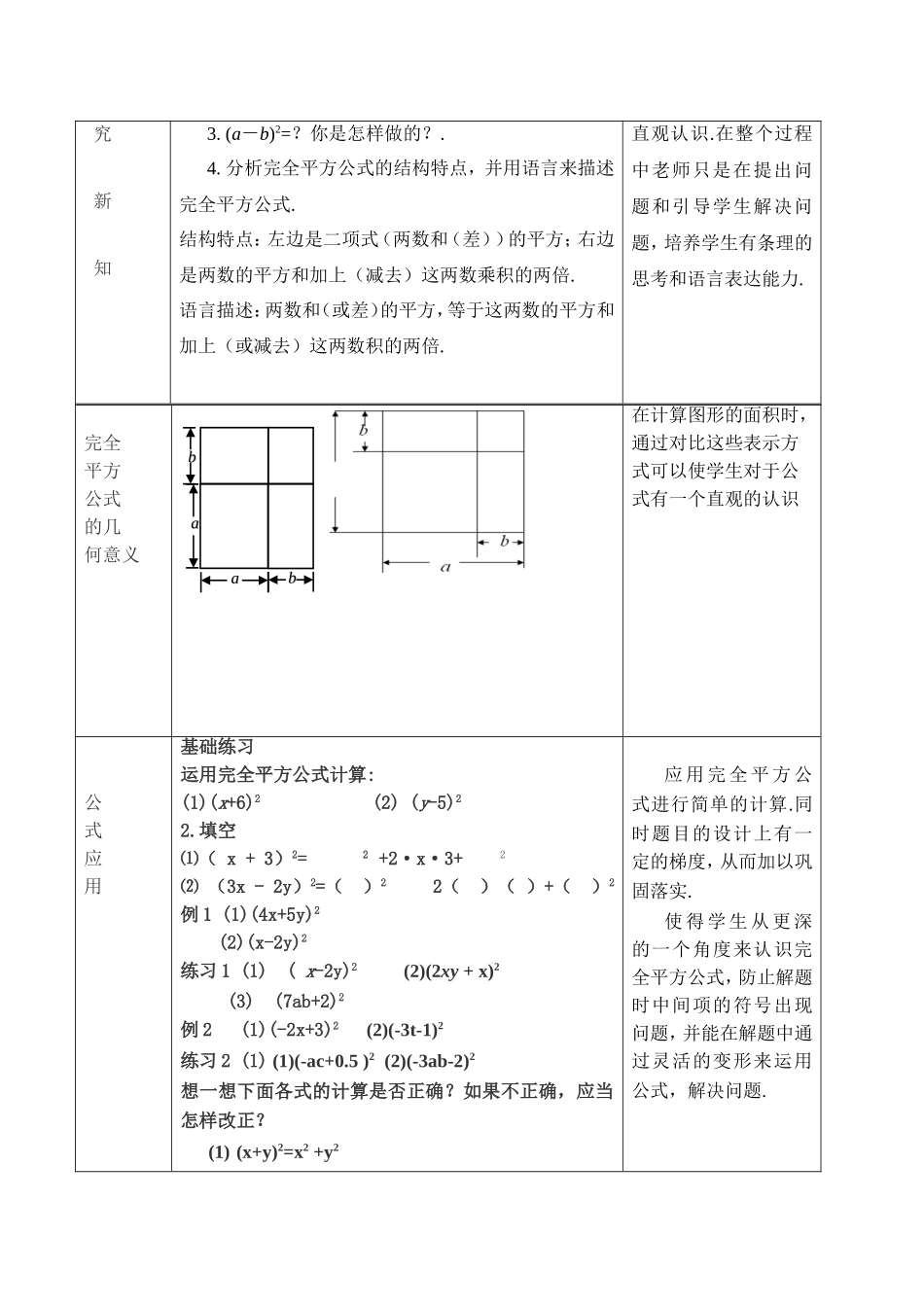
完全平方公式(1)教学目标1.知识与技能:理解公式的本质,从不同的层次上理解完全平方公式,并会运用公式进行简单的计算,了解完全平方公式的几何背景2.过程与方法:经历探索完全平方公式的过程,并从推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力,发展逻辑推理能力和有条理的表达能力,培养学生的数形结合意识.3.情感与态度:在学习中使学生体会学习数学的乐趣,培养学习数学的信心,感受数学的内在美.教学重难点重点:理解完全平方公式,正确运用完全平方公式进行简单计算.难点:感悟换元变换的思想方法,正确运用完全平方公式.教学方法:引导探究,讲练结合教学过程教学环节师生活动设计意图复习回顾1.平方差公式:(a+b)(a-b)=a2-b2;2.公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积.右边是两数的平方差.3.应用平方差公式的注意事项:弄清在什么情况下才能使用平方差公式..平方差公式的学习有很多教学环节和形式与本节的学习是类似的,其中包含的基本知识与基本能力也仍是本节的精神主旨,因而复习很有必要.探1.计算下列算式,你有什么发现?(1)(P+1)2=______(2)(m+3)2=________(3)(2+3x)2=________猜想(a+b)2=?2.用多项式乘以多项式的法则验证(a+b)2=?并用自己的语言叙述这一公式通过特例的探索,引入完全平方公式,加深对公式的体会.从而在学生的自主探索过程中验证了完全平方公式,使学生有了一个究新知3.(a-b)2=?你是怎样做的?.4.分析完全平方公式的结构特点,并用语言来描述完全平方公式.结构特点:左边是二项式(两数和(差))的平方;右边是两数的平方和加上(减去)这两数乘积的两倍.语言描述:两数和(或差)的平方,等于这两数的平方和加上(或减去)这两数积的两倍.直观认识.在整个过程中老师只是在提出问题和引导学生解决问题,培养学生有条理的思考和语言表达能力.完全平方公式的几何意义在计算图形的面积时,通过对比这些表示方式可以使学生对于公式有一个直观的认识公式应用基础练习运用完全平方公式计算:(1)(x+6)2(2)(y-5)22.填空⑴(x+3)2=2+2·x·3+2⑵(3x-2y)2=()22()()+()2例1(1)(4x+5y)2(2)(x-2y)2练习1(1)(x-2y)2(2)(2xy+x)2(3)(7ab+2)2例2(1)(-2x+3)2(2)(-3t-1)2练习2(1)(1)(-ac+0.5)2(2)(-3ab-2)2想一想下面各式的计算是否正确?如果不正确,应当怎样改正?(1)(x+y)2=x2+y2应用完全平方公式进行简单的计算.同时题目的设计上有一定的梯度,从而加以巩固落实.使得学生从更深的一个角度来认识完全平方公式,防止解题时中间项的符号出现问题,并能在解题中通过灵活的变形来运用公式,解决问题.bbbbaaaa(2)(x-y)2=x2-y2(3)(-x+y)2=x2+2xy+y2(4)(2x+y)2=4x2+2xy+y2拓展计算(a+b+c)2课堂小结1.熟记完全平方公式2.在解题过程中要准确确定a和b,对照公式原形的两边,做到不丢项、不弄错符号、2ab时不少乘2作业:配套练习完全平方公式1