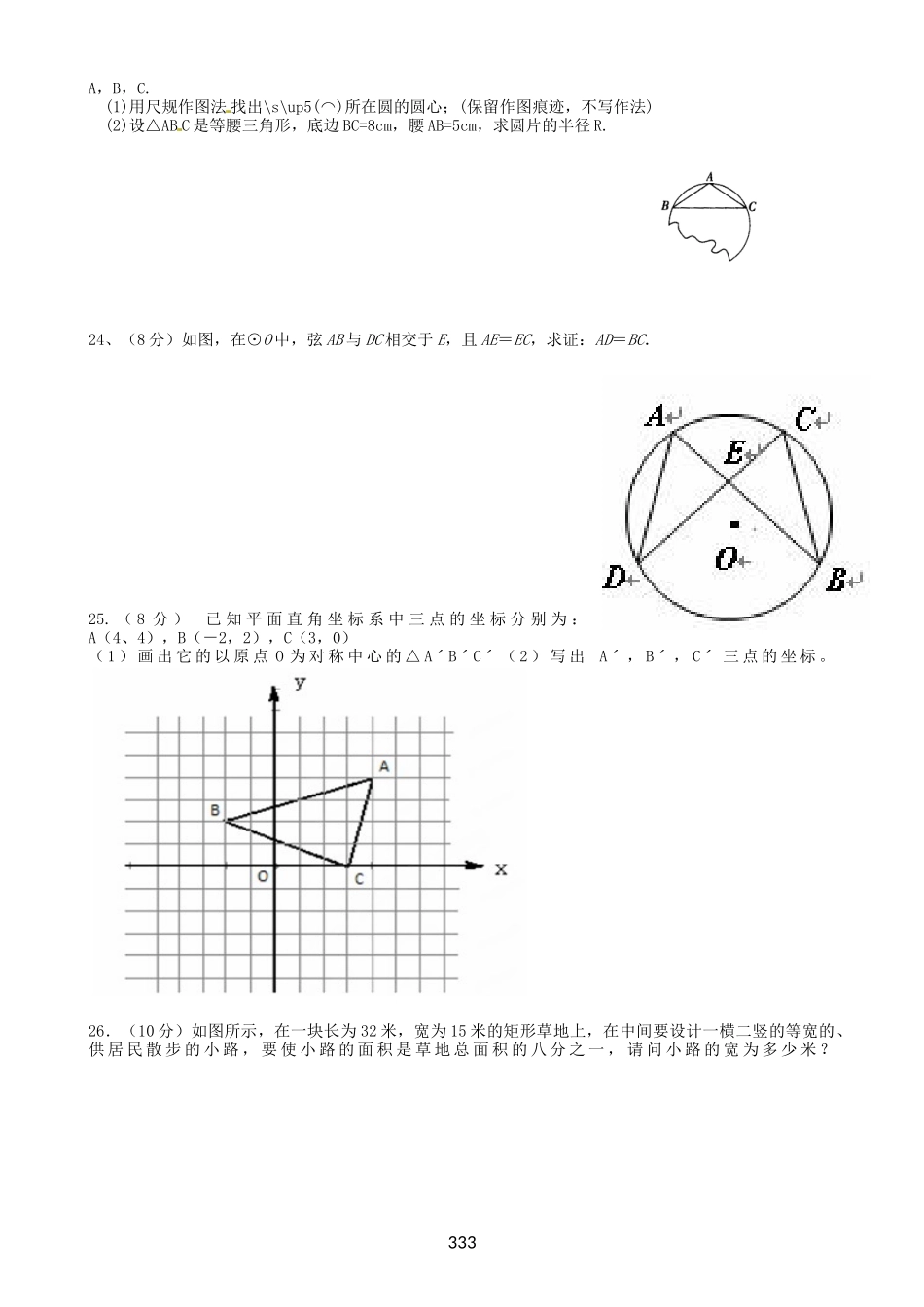
0122xx九年级数学上学期期中考试题一、选择题(每题3分,共30分)1.下面有4个汽车标志图案,其中是中心对称图形的是()A、④B.③C、②D、①2.下列函数中,不是二次函数的是()A.y=1-x2B.y=2(x-1)2+4C.y=(x-1)(x+4)D.y=(x-2)2-x23.下列方程中是一元二次方程的是().A.xy+2=1B.x2+12x−9=0C.ax2+bx+c=0D.x2=04.对抛物线y=-x2+2x-3而言,下列结论正确的是()A.与x轴有两个交点B.开口向上C.与y轴的交点坐标是(0,3)D.顶点坐标是(1,-2)5.若点A(n,2)与点B(-3,m)关于原点对称,则n-m=()A.-1B.-5C.1D.56.将一元二次方程(3x−2)(x+1)=x(2x−1)化成一般形式后,它的一次项系数是()A.−2B.2C.−3D.−17.方程的根的情况是()A、有两个不等实数根B、有两个相等实数根C、无实数根D、无法判定8.⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P()A.在⊙O内B.在⊙O上C.在⊙O外D.可能在⊙O上或在⊙O内9.如图,在⊙O中,∠ABC=50°,则∠AOC等于()A.50°B.80°C.90°D.100°10.在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是()二、填空题(每题3分,共30分)11.方程,化为一般形式为________________,12.如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:①四边形ABCD是菱形;②四边形ABCD是中心对称图形;③四边形ABCD是轴对称图形;④AC=BD.其中正确的是________(写正确的111序号)13.设一元二次方程的两个实数分别为和,则,。14.点A(-2,b)与点B(a,4)关于y轴对称,则a+b=.15.如下图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=________.16.如下图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A=______,∠B=______,∠C=______.17.如果一元二方程(m−2)x2+3x+m2−4=0有一个根为0,则m=.18.△ABC内接于⊙O,∠ACB=36°,那么∠AOB的度数为__________19.已知二次函数的图象过(1,0),(2,0)和(0,2)三点,则该函数的解析式是.20.如下图,Rt△ABC分别绕直角边AB,BC旋转一周,旋转后得到的两个圆锥的母线长分别为____________.三、解答题(共60分)21、解下列方程:(8分)(1)2410xx(用配方法);(2)22、(8分)已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线23、(8分)如图所示,要把残破的轮片复制完整,已知弧上的三点A,B,C.(1)用尺规作图法找出\s\up5(⌒)所在圆的圆心;(保留作图痕迹,不写作法)(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.24、(8分)如图,在⊙O中,弦AB与DC相交于E,且AE=EC,求证:AD=BC.25.(8分)已知平面直角坐标系中三点的坐标分别为:A(4、4),B(-2,2),C(3,0)(1)画出它的以原点O为对称中心的△AˊBˊCˊ(2)写出Aˊ,Bˊ,Cˊ三点的坐标。26.(10分)如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽为多少米?33327、(10分)如图,已知抛物线与轴交于、两点,与轴交于点⑴求、、三点的坐标,⑵过点作交抛物线于点,求△APC的面积xyOPCBA参考答案:1——5ADDDD6——10CABDC11、x2-2x-9=0x2-2-912、①②③13、6414、615、40°16、50°60°70°17、-218、72°19、y=x2-3x+220、2221、略22、解:连接OD,证三角形OCD全等于三角形OCB23、(2)25/624、证三角形ADE全等于三角形CBE25、解:(2)A(-4,-4)B(2,2)C(-3,0)′′′26、1米27、解:(1)A(-1,0)B(1,0)C(0,-1)(2)三角形的面积为3