指数函数 (2)VIP免费

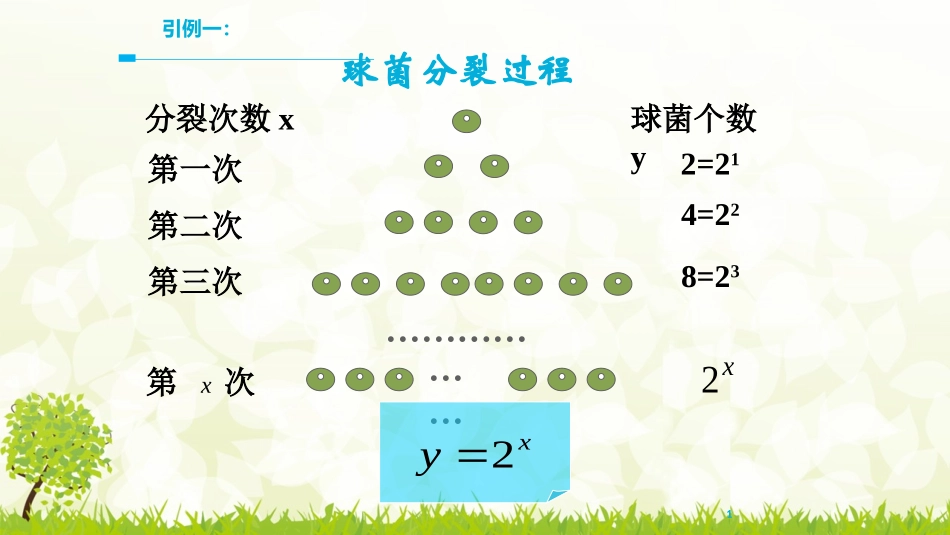
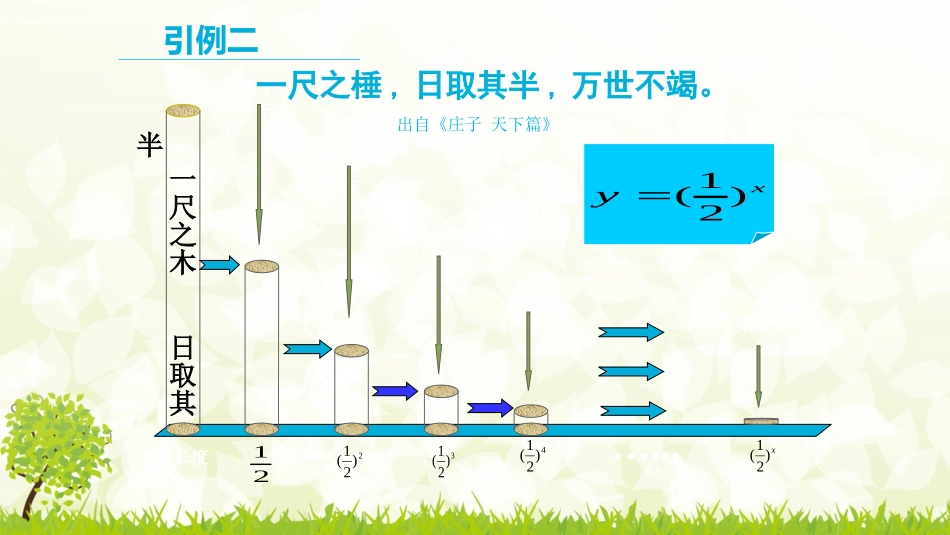
2.1指数函数引例一：1球菌分裂过程分裂次数x第一次第二次球菌个数y2=214=228=23…………第x次……x2xy2第三次…...剩余长度yxy)21(一尺之木日取其半第1次后第2次后第3次后第4次后第x次后212)21(3)21(4)21(x)21(引例二一尺之棰,日取其半,万世不竭。出自《庄子天下篇》仔细观察，函数解析式的共同特征?；xy2)1(xy)21()2(思考:定义：3函数叫做指数函数，函数的定义域是R．x其中是自变量．xay)1,0(aa且概念解析4呢？且为什么要10aa01a0时，①若a=0，则当x>0时，xa=0；xa无意义.当x②若a<0，则对于x的某些数值，可使xa无意义.如x)2(，这时对于x=41，x=21等等，在实数范围内函数值不存在.③若a=1，则对于任何xR，xa=1，是一个常量，没有研究的必要性.为了避免上述各种情况，所以规定a>0且a1。下面的式子是不是指数函数？5练习1：xy23反思：你能说出指数函数的结构特征吗？系数为1指数是未知数底数大于零不得1123判断下列函数是否是指数函数23xy13xy3xyxy3)121()12(aaayx，且xy)4(xy24xyxxy2(232)()0,1()111()()122xyaaaaAaaBaCaDaa练习：函数是指数函数，则的取值范围是（）或A-2-1.5-1-0.500.511.52二、作出函数的图象（重点）xy2xy21xy.........0.350.250.71422.8311.410.50-2-1.5-1-0.500.511.5242.8321.4110.710.50.350.25xy)21(011xy.........图象二、作出函数的图象（重点）xy)21(yx0·(0,1)指数函数的图象和性质1.定义域:2.值域:3.过点:4.单调性:5.函数值的变化情况:当x<0时,00时,y>1.a＞10＜a＜1图象性质在R上是在R上是x＞0时，ax＞1;x＜0时，0＜ax＜1x＞0时，0＜ax＜1;x＜0时，ax＞1指数函数的图象和性质：y＝1xyy＝ax(a＞1)Oy＝1xyy＝ax(0＜a＜1)O(0,1)(0,1))10(aaayx且定义域R；值域(0，＋∞)过点(0，1)，即x＝0时，y＝1增函数减函数随着X增大，函数值也增大随着X增大，函数值也增大例1、比较大小:35.27.1,7.1)1(01xyxy7.1所以.7.17.135.201xyxy8.0随着X增大，函数值在减小随着X增大，函数值在减小2.01.08.0,8.0)2(所以.8.08.02.01.0所以1.33.09.07.1（3）解：根据指数函数的性质，得：17.13.019.01.33.232.82.62.42.221.81.61.41.210.80.60.40.2-0.2-0.4-0.50.511.522.533.54fx=0.9x3.232.82.62.42.221.81.61.41.210.80.60.40.2-0.2-0.4-2-1.5-1-0.50.511.522.5fx=1.7x方法总结：1.利用指数函数的单调性，必须要明确所给的两个值是哪个指数函数的两个函数值。数的特征是同底不同指。2.中间值比较法：用别的中间数如0或1做桥。数的特征是不同底不同指。1.比较幂大小的方法(1)对于同底数不同指数的两个幂的大小，利用指数函数的性来判断；(2)对于底数不同指数也不同的两个幂的大小，则通过来判断．单调中间值方法总结：01xyxy2xy21xy3xy31xy31xy21深入探究，加深理解（难点）深入探究，加深理解（难点）在第一象限沿箭头方向底增大在第一象限沿箭头方向底增大观察图像，发现图像与底的关系观察图像，发现图像与底的关系比较下列两个数的大小：(23)－0.5，(34)－0.5；在同一平面直角坐标系中画出指数函数y＝(23)x与y＝(34)x的图象，当x＝－0.5时，观察图象可得(23)－0.5＞(34)－0.5.1.比较幂大小的方法(1)对于同底数不同指数的两个幂的大小，利用指数函数的性来判断；(2)对于底数不同指数也不同的两个幂的大小，则通过来判断．(3)对于底数不同指数相同的两个幂的大小，利用指数函数的的变化规律来判断；单调图象中间值例2、指数函数,,,xxxxyaybycyd的图象如下图所示，则底数,,,abcd与正整数1共五个数，从大到小的顺序是：.xy01xyaxybxydxyc01badc1badc例3.解不等式：142).1(xx)10().2(4213aaaaxx且函数f(x)＝a322xx＋m(a>1)恒过点(1,10)，则m＝______.解析f(x)＝a322xx＋m在x2＋2x－3＝0时过定点(1，1＋m)或(－3,1＋m)，∴1＋m＝10，解得m＝9.9概念延伸指数函数定义指数函数图像指数函数定义指数函数图像指数函数性质比较不同数大小课堂小结：研究函数:定义→图象→性质→应用数形结合的数学思想会比较简单的同底数指数的大小指数函数的概念、图象和性质；分类讨论的数学思想课堂小结