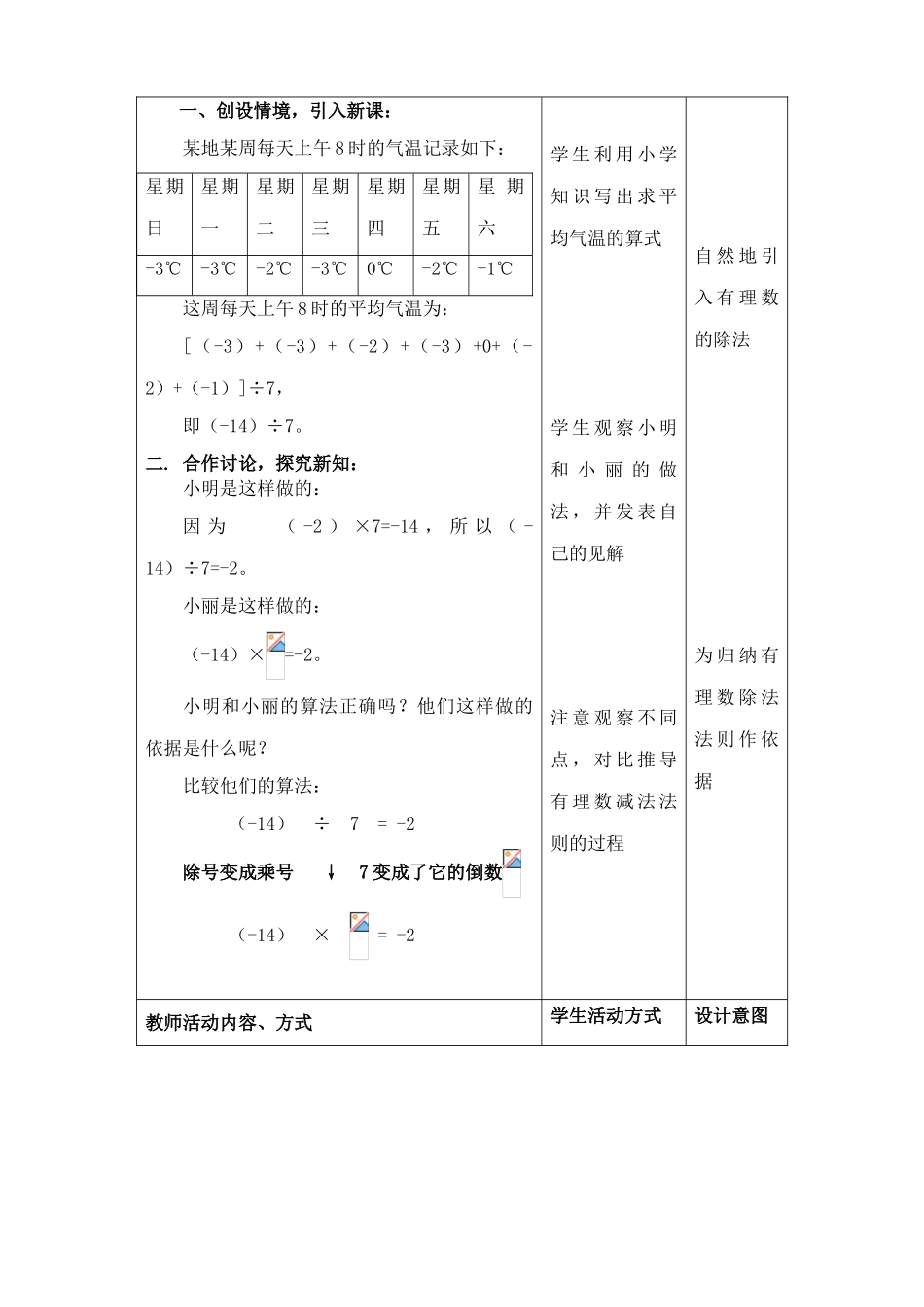
总课题有理数总课时课题有理数的乘法与除法第三课时课型新授课教学目标1.使学生理解有理数乘法的意义;2.使学生掌握有理数的除法法则,能够熟练地进行除法运算;3.培养学生观察、归纳、概括及运算能力.教学重点有理数除法法则.教学难点商的符号的确定.教具准备实物投影仪教学过程教学内容教师活动内容、方式学生活动方式设计意图一、创设情境,引入新课:某地某周每天上午8时的气温记录如下:星期日星期一星期二星期三星期四星期五星期六-3℃-3℃-2℃-3℃0℃-2℃-1℃这周每天上午8时的平均气温为:[(-3)+(-3)+(-2)+(-3)+0+(-2)+(-1)]÷7,即(-14)÷7。二.合作讨论,探究新知:小明是这样做的:因为(-2)×7=-14,所以(-14)÷7=-2。小丽是这样做的:(-14)×=-2。小明和小丽的算法正确吗?他们这样做的依据是什么呢?比较他们的算法:(-14)÷7=-2除号变成乘号↓7变成了它的倒数(-14)×=-2学生利用小学知识写出求平均气温的算式学生观察小明和小丽的做法,并发表自己的见解注意观察不同点,对比推导有理数减法法则的过程自然地引入有理数的除法为归纳有理数除法法则作依据教师活动内容、方式学生活动方式设计意图则:(-14)÷7=(-14)×下列各式中两数相除的商是多少?你用什么方法验算。(1)(-10)÷2(2)24÷(-8)(3)(-12)÷(-4)思考:小学知识中0能否作为除数?归纳:有理数除法法则:除以一个不等于0的数,等于乘以这个数的倒数。说明:有理数的除法可以转化为乘法,因此有理数的除法还有如下法则:两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个不等于0的数,都得0三、应用举例,变式练习:填一填:(1)8÷(-2)=8×;(2)6÷(-3)=6×;(3)-6÷=-6×(4)-6÷=-6×;做一做:(1)5的倒数是;(2)2的倒数是;(3)0.1的倒数是;(4)-3.75的倒数是;(5)-3的倒数是;(6)-0.15的倒数是;例4:计算:(1)36÷(-9)(2)(-48)÷(-6)(3)(-32)÷4×(-8)(4)17×(-6)÷(-5)联想有理数减法法则,尝试归纳有理数除法法则对照有理数乘法法则,理解有理数除法法则学生口答教师写出范例(1)学生板演(2)(3)(4)说出两个有理数相除,商的符号是怎样确用来检验学生总结的结论是否具有一般性提示学生0不能作为除数为除法转化为乘法做铺垫进一步巩固有理数除法法则练习:化简:(1)=;(2)=;(3)=;(4)=;定的,商的绝对值又是如何确定的。教师活动内容、方式学生活动方式设计意图例5计算:(1)()÷()(2)(-81)÷×÷(-16)四、课堂小结:本节课你的收获是什么?(有理数除法的两个运算法则)五、作业:见作业纸学生板演,注意运算顺序学生尝试小结,其他学生给予补充培养学生综合能力与运算能力