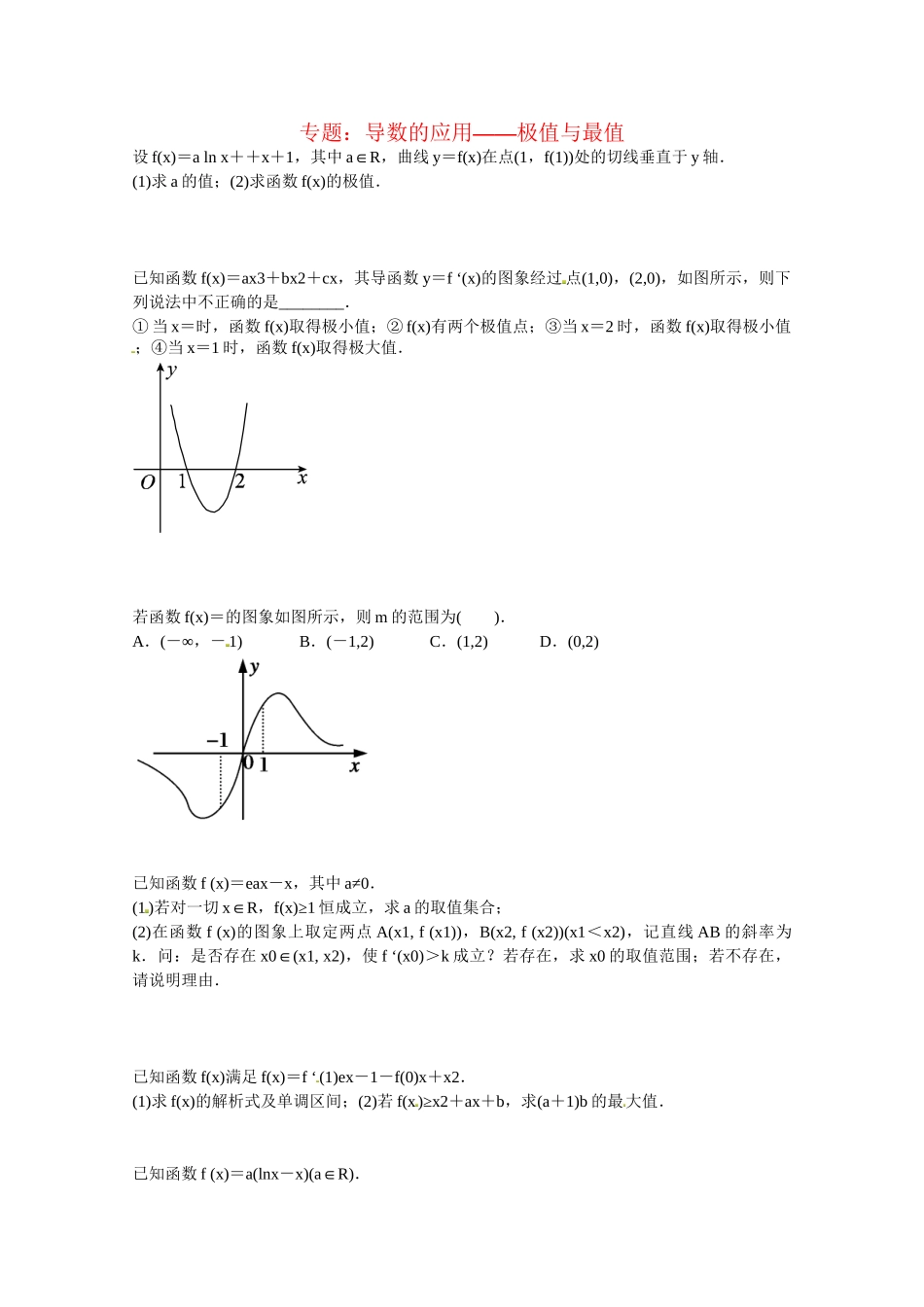
——专题:导数的应用极值与最值设f(x)=alnx++x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.(1)求a的值;(2)求函数f(x)的极值.已知函数f(x)=ax3+bx2+cx,其导函数y=f‘(x)的图象经过点(1,0),(2,0),如图所示,则下列说法中不正确的是________.①当x=时,函数f(x)取得极小值;②f(x)有两个极值点;③当x=2时,函数f(x)取得极小值;④当x=1时,函数f(x)取得极大值.若函数f(x)=的图象如图所示,则m的范围为().A.(∞-,-1)B.(-1,2)C.(1,2)D.(0,2)已知函数f(x)=eax-x,其中a≠0.(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合;(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k.问:是否存在x0∈(x1,x2),使f‘(x0)>k成立?若存在,求x0的取值范围;若不存在,请说明理由.已知函数f(x)满足f(x)=f‘(1)ex-1-f(0)x+x2.(1)求f(x)的解析式及单调区间;(2)若f(x)≥x2+ax+b,求(a+1)b的最大值.已知函数f(x)=a(lnx-x)(a∈R).(1)讨论函数f(x)的单调性;(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,函数g(x)=x3+x2在区间(2,3)上总存在极值,求实数m的取值范围.已知函数f(x)=x3+ax2+bx+a2在x=1处取极值10,则f(2)=________.课后练习详解答案:(1)a=-1;(2)极小值f(1)=3,无极大值.详解:(1)因f(x)=alnx++x+1,故f‘(x)=-+.由于曲线y=f(x)在点(1,f(1))处的切线垂直于y轴,故该切线斜率为0,即f‘(1)=0,从而a-+=0,解得a=-1.(2)由(1)知f(x)=-lnx++x+1(x>0),f‘(x)=--+==.令f‘(x)=0,解得x1=1,x2=-(因x2=-不在定义域内,舍去).当x∈(0,1)时,f‘(x)<0,故f(x)在(0,1)上为减函数;当x∈(1∞,+)时,f‘(x)>0,故f(x)在(1∞,+)上为增函数.故f(x)在x=1处取得极小值f(1)=3,无极大值.答案:①.详解:从图象上可以看到:当x∈(∞-,1)时,f‘(x)>0;当x∈(1,2)时,f‘(x)<0;当x∈(2,∞+)时,f‘(x)>0,所以f(x)有两个极值点1和2,且当x=2时函数取得极小值,当x=1时函数取得极大值.只有①不正确.答案:C.详解:f‘(x)==由图知m-2<0,且m>0,故0<m<2,又>1,∴m>1,因此1<m<2,选C.答案:(1){1};(2)x0的取值范围为.详解:(1)若a<0,则对一切x>0,f(x)=eax-x<1,这与题设矛盾.又a≠0,故a>0.而f‘(x)=aeax-1,令f‘(x)=0得x=ln.当x<ln时,f‘(x)<0,f(x)单调递减;当x>ln时,f‘(x)>0,f(x)单调递增.故当x=ln,f(x)取最小值f=-ln.于是对一切x∈R,f(x)≥1恒成立,当且仅当-ln≥1.①令g(t)=t-tlnt,则g‘(t)=-lnt.当0<t<1时,g‘(t)>0,g(t)单调递增;当t>1时,g‘(t)<0,g(t)单调递减.故当t=1时,g(t)取最大值g(1)=1.因此,当且仅当=1,即a=1时,①式成立.综上所述,a的取值集合为{1}.(2)由题意知,k==2121axaxeexx-1.令φ(x)=f‘(x)-k=aeax-2121axaxeexx.则φ(x1)=-211axexx[21()axxe-a(x2-x1)-1],φ(x2)=212axexx[12()axxe-a(x1-x2)-1].令F(t)=et-t-1,则F‘(t)=et-1.当t<0时,F‘(t)<0,F(t)单调递减;当t>0时,F‘(t)>0,F(t)单调递增.故当t≠0时,F(t)>F(0)=0,即et-t-1>0.从而21()axxe-a(x2-x1)-1>0,12()axxe-a(x1-x2)-1>0,又211axexx>0,212axexx>0,所以φ(x1)<0,φ(x2)>0.因为函数y=φ(x)在区间[x1,x2]上的图象是连续不断的一条曲线,所以存在c∈(x1,x2),使得φ(c)=0.又φ‘(x)=a2eax>0,φ(x)单调递增,故这样的c是唯一的,且c=21211ln()axaxeeaaxx.故当且仅当x∈时,f‘(x)>k.综上所述,存在x0∈(x1,x2),使f‘(x0)>k成立,且x0的取值范围为.答案:(1)(a+1)b的最大值为.详解:(1)由已知得f‘(x)=f‘(1)ex1-f(0)+x.所以f‘(1)=f‘(1)-f(0)+1,即f(0)=1.又f(0)=f‘(1)e1,所以f‘(1)=e.从而f(x)=ex-x+x2.由于f‘(x)=ex-1+x,故当x∈(∞-,0)时,f‘(x)<0;当x∈(0∞,+)时,f‘(x)>0.从而,f(x)在(∞-,0)单调递...