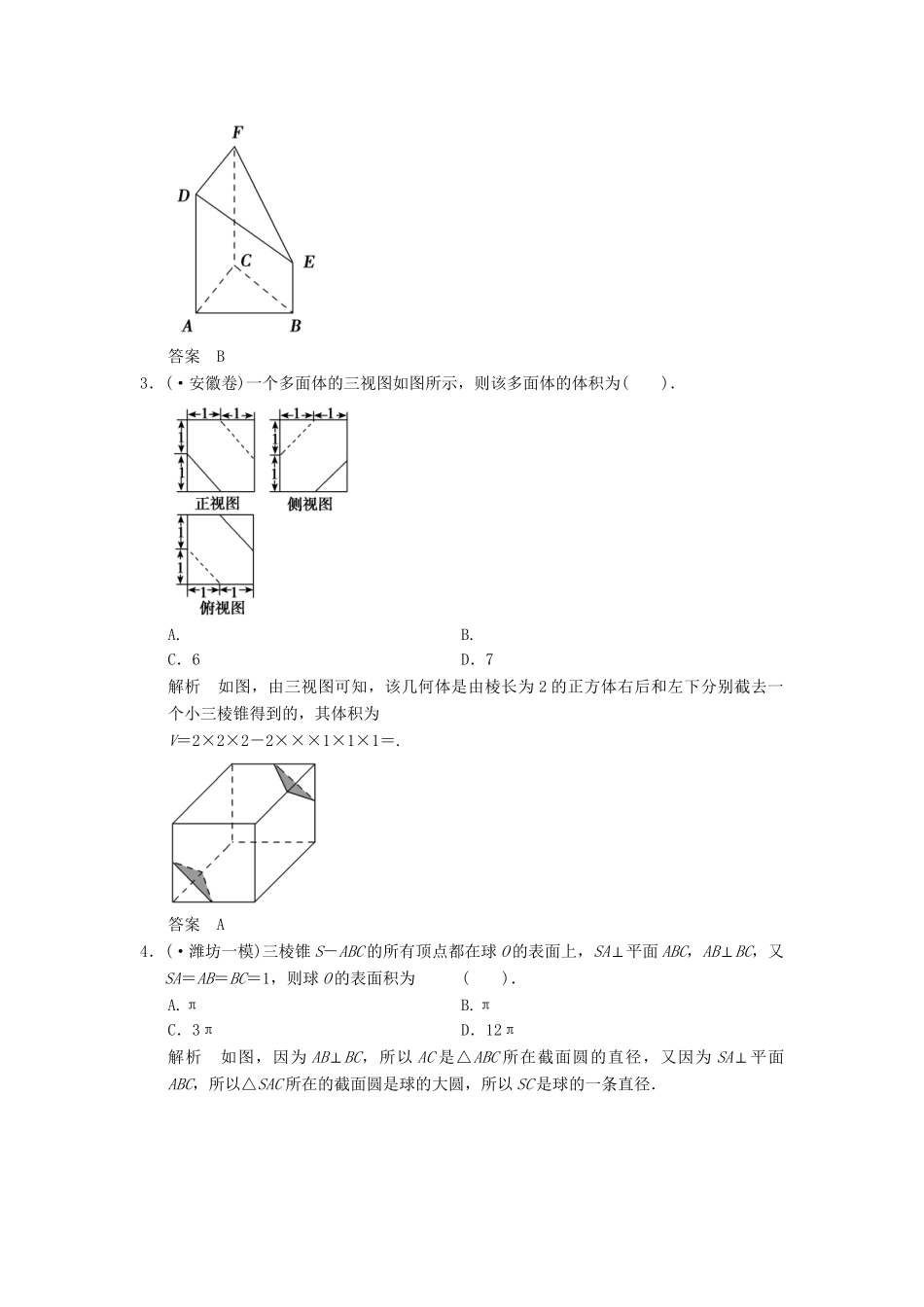
【创新设计】(人教通用)高考数学二轮复习专题整合4-1立体几何的基本问题(计算与位置关系)理(含最新原创题,含解析)一、选择题1.(·广东卷)若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是().A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定解析构造如图所示的正方体ABCD-A1B1C1D1,取l1为AD,l2为AA1,l3为A1B1,当取l4为B1C1时,l1∥l4,当取l4为BB1时,l1⊥l4,故排除A、B、C,选D.答案D2.(·重庆卷)某几何体的三视图如图所示,则该几何体的表面积为().A.54B.60C.66D.72解析还原为如图所示的直观图,S表=S△ABC+S△DEF+S矩形ACFD+S梯形ABED+S梯形CBEF=×3×4+×3×5+5×3+×(2+5)×4+×(2+5)×5=60.答案B3.(·安徽卷)一个多面体的三视图如图所示,则该多面体的体积为().A.B.C.6D.7解析如图,由三视图可知,该几何体是由棱长为2的正方体右后和左下分别截去一个小三棱锥得到的,其体积为V=2×2×2-2×××1×1×1=.答案A4.(·潍坊一模)三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=1,则球O的表面积为().A.πB.πC.3πD.12π解析如图,因为AB⊥BC,所以AC是△ABC所在截面圆的直径,又因为SA⊥平面ABC,所以△SAC所在的截面圆是球的大圆,所以SC是球的一条直径.由题设SA=AB=BC=1,由勾股定理可求得:AC=,SC=,所以球的半径R=,所以球的表面积为4π×2=3π.答案C二、填空题5.(·金丽衢十二校联考)一个几何体的三视图如图所示,则该几何体的体积为________.解析由题意可得,几何体相当于一个棱长为2的正方体切去一个角,角的相邻三条棱长分别是1,2,2,所以几何体的体积为8-=.答案6.(·山东卷)一个六棱锥的体积为2,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.解析设棱锥的高为h,则V=×S底·h=×6××22×h=2,∴h=1,由勾股定理知,侧棱长为=, 六棱锥六个侧面全等,且侧面三角形的高为=2,∴S侧=×2×2×6=12.答案127.(·武汉调研测试)已知某几何体的三视图如下图所示,则该几何体的表面积为________.解析由三视图可知,该几何体是底面半径为1,高为,母线长为2的圆锥的一半,其表面积是整个圆锥表面积的一半与轴截面的面积之和.所以,S=××2π×1×2+×π×12+×2×=+.答案+8.正方体ABCD-A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中正确的是________(填序号).①AC⊥BE;②B1E∥平面ABCD;③三棱锥E-ABC的体积为定值;④直线B1E⊥直线BC1.解析因AC⊥平面BDD1B1,故①正确;易得②正确;记正方体的体积为V,则VE-ABC=V为定值,故③正确;B1E与BC1不垂直,故④错误.答案①②③三、解答题9.如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE.证明(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE⊄平面A1CB,BC⊂平面A1CB,所以DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD,又A1D∩CD=D,所以DE⊥平面A1DC.而A1F⊂平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,DE∩CD=D,所以A1F⊥平面BCDE.又 BE⊂平面BCDE,所以A1F⊥BE.10.(·威海一模)如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.(1)求证:平面ADF⊥平面CBF;(2)求证:PM∥平面AFC;(3)求多面体CD-AFEB的体积V.(1)证明 矩形ABCD所在的平面和平面ABEF互相垂直,且CB⊥AB,∴CB⊥平面ABEF,又AF⊂平面ABEF,所以CB⊥AF,又AB=2,AF=1,∠BAF=60°,由余弦定理知BF=,∴AF2+BF2=AB2,得AF⊥BF,BF∩CB=B,∴AF⊥平面CFB,又 AF⊂平面ADF;∴平面ADF⊥平面CBF.(2)证明连接OM延长交BF于H,则H为BF的中点,又P为CB的中点,∴PH∥CF,又 CF⊂平面AFC,PH⊄平面AFC,∴PH∥平面AFC,连接PO,则PO∥AC,又 AC⊂平面AFC,PO⊄平面AF...