全等AAS、SSSVIP免费

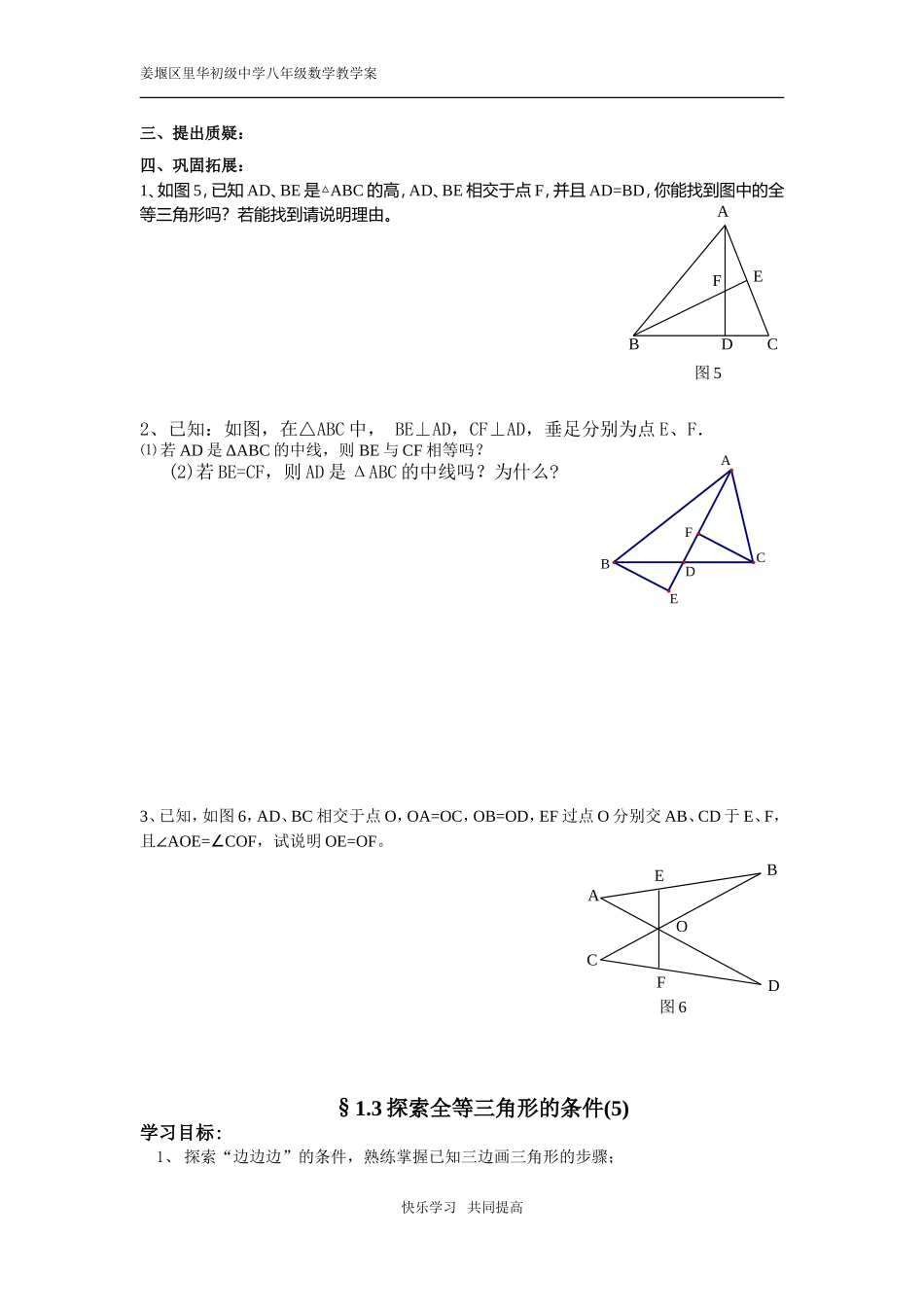
姜堰区里华初级中学八年级数学教学案§1.3探索三角形全等的条件（4）学习目标：1.掌握三角形全等的“角边角”，“角角边”条件。2.在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理。学习重点：探索三角形全等的“角边角”、“角角边”的条件来判别两个三角形是否全等，并能解决一些简单的实际问题一、预习导航如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF，△ABC和△DEF全等吗？为什么？结论：二、合作探究：1、已知，如图3，∠1＝∠2，∠C＝∠D，AD=EC，△ABD≌△EBC吗？为什么？2、已知，如图4、点A、F、E、C在同一条直线上，AF＝CE，BE∥DF，AB∥CD。试说明：△ABE≌△CDF快乐学习共同提高ABCDE12图3ABCDEF图4姜堰区里华初级中学八年级数学教学案三、提出质疑：四、巩固拓展：1、如图5，已知AD、BE是△ABC的高，AD、BE相交于点F，并且AD=BD，你能找到图中的全等三角形吗？若能找到请说明理由。2、已知：如图，在△ABC中，BE⊥AD，CF⊥AD，垂足分别为点E、F．⑴若AD是ΔABC的中线，则BE与CF相等吗？(2)若BE=CF，则AD是ΔABC的中线吗？为什么?3、已知，如图6，AD、BC相交于点O，OA=OC，OB=OD，EF过点O分别交AB、CD于E、F，且∠AOE=∠COF，试说明OE=OF。§1.3探索全等三角形的条件(5)学习目标:1、探索“边边边”的条件，熟练掌握已知三边画三角形的步骤；快乐学习共同提高FEOACDB图6ABCEFD图5EFDBCACBAEDBACDEF姜堰区里华初级中学八年级数学教学案2、了解三角形的稳定性、四边形的不稳定性，以及它们在生活中的应用，感受数学的价值，增强应用数学的意识，学会用数学的眼光去观察、分析周围的事物。学习重点：“边边边”条件的探索及应用；一、预习导航小明用长度分别是5cm,6cm,7cm的3根木棒搭出了三角形ABC,试问:小丽应选用怎么样大小的3根木棒能使她搭出的三角形MPN与三角形ABC全等?每一位学生按下列步骤作图1.画线段AB=4cm.2.分别以点A点B为圆心,3cm,2cm的长为半径画弧,两弧相交于点C.3.连接AC、BC作图区域归纳三角形全等的条件：思考：三角形为什么具备稳定性？有什么办法让四边形也具备稳定性？二、合作探究：1.已知:如图，AB=AC，BD=CD，△ABD与△ACD全等吗？为什么？2．如图，已知AB＝AE，AC＝AD，BC＝DE，试说明∠CAE＝∠DAB．3．如图，点A、F、C、D在一直线上，AB＝DE，AF＝CD，BC＝EF．请说明：（1）△ABC≌△DEF；（2）∠CBF＝∠FEC．（提示：根据条件，仔细观察图形，找准全等的三角形）快乐学习共同提高ABCD姜堰区里华初级中学八年级数学教学案三、提出质疑：四、巩固拓展：1、如图，在ΔABC中，AB=AC求证：∠B=∠C2、如图，在ΔABC与ΔAED中，AB=AE，AC=AD，请补充一个已知条件：____________(写一个即可)，使ΔABC≌ΔAED.并说明理由.3、如图，AD、A/D/分别是ΔABC与ΔA/B/C/中BC、B/C/边上的高，且AB＝A/B/，AD＝A/D/．若使ΔABC≌ΔA/B/C/，请你补充条件（只需填写一个你认为适当的条件）并证明你的结论.快乐学习共同提高EABCDA′B′C′D′ABCD