勾股定理教学课件VIP免费

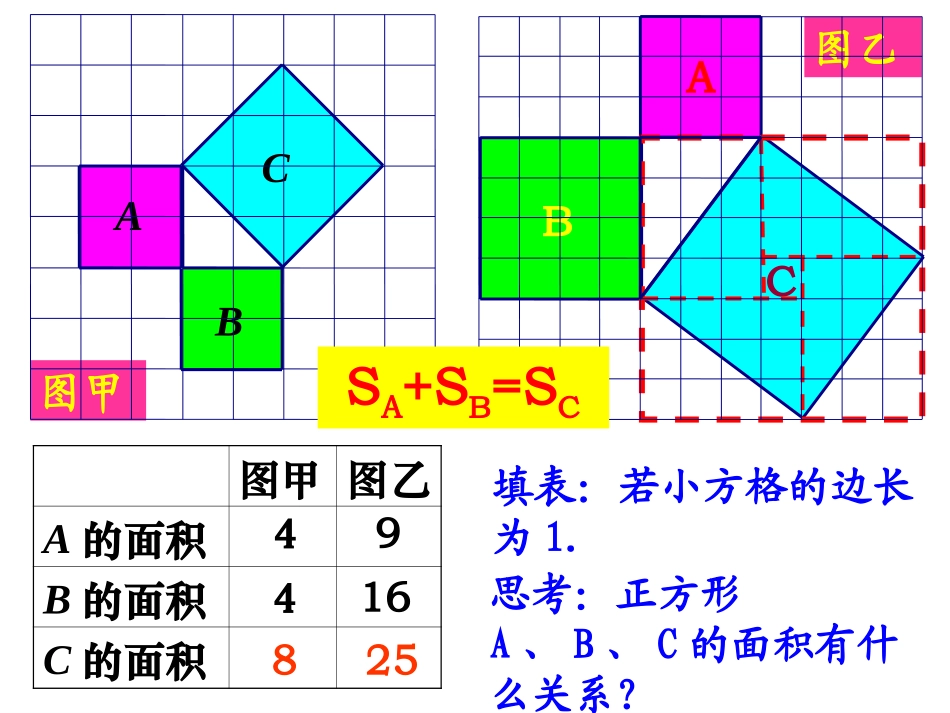
2002年国际数学家大会在北京召开，左下图是本届的会标,它是赵爽弦图。与勾股定理有关，数学家曾建议用勾股定理的图来作为与“外星人”联系的信号。2002年国际数学家大会在北京召开，左下图是本届的会标,它是赵爽弦图。与勾股定理有关，数学家曾建议用勾股定理的图来作为与“外星人”联系的信号。相传2500年前，毕达哥拉斯有一次在朋友家里做客时，通过朋友铺地的成的地面中反映了直角三角形三边的某种数量关系．我们也来观察右图中的地面，看看有什么发现？ABC填表：若小方格的边长为1.图甲图甲图乙A的面积B的面积C的面积CABC思考：正方形A、B、C的面积有什么关系？44891625图乙SA+SB=SCAB图乙SA+SB=SCABC图甲abcabcC猜想:a、b、c之间的关系？a2+b2=c2问题：边长为任意长度的直角三角形还成立吗？验证:a、b、c之间的关系？a2+b2=c2a用拼图法证明验证:a、b、c之间的关系？a2+b2=c2bcbacbaaabbc方法1：S大正方形=c2方法2：S大正方形=4S直角三角形+S小正方形=a2+b2214()2abba验证:a、b、c之间的关系？a2+b2=c2abc用拼图法证明∴a2+b2=c2bcaacbabab2222abbabaab?勾股定理如果直角三角形两直角边分别为a，b，斜边为c，那么即直角三角形两直角边的平方和等于斜边的平方.222cbaac勾弦b股归纳定理：勾股强调：勾股定理反映了直角三角形的三边关系。(毕达哥拉斯定理)34511、、cc22=a=a22+b+b22abc确定斜边33、、bb22=c=c22-a-a2222、、aa22=c=c22-b-b223322++4422==5522灵活运用公式？变式运用：22cab即22cb即a22bca即填空：在Rt△ABC中，∠Ｃ=90°.(1)若：a=6，ｂ=8，则c=；(2)若：c=13，b=12，则a=；（3）若：a=,c=,则b=;试一试:75510211解：解：运用勾股定理运用勾股定理在四边形在四边形ABCDABCD中，∠中，∠DABDAB＝∠＝∠DBCDBC＝＝90º90ºADAD＝＝33，，ABAB＝＝44，，BCBC＝＝1212求：求：DCDC的长。的长。例：例：BBCCDDAA在直角三角形中,已知两边,可求第三边;方法小结02222290RtABDBDAD+AB=3+4=25BD=255DC13DAB在中，同理可得：练习1、已知：Rt△ABC中，AB＝４，AC＝３,则BC的长为.5或7试一试:43CAB？43ACB？6班练习2、在直角三角形ABC中,C=90°∠，（1）已知∠Ａ＝３０°,ａ＝３，则b=.c=；（2）已知∠Ａ＝４５°，ｃ＝８，则a=.b=；试一试:3364242(3)已知:a:b=3:4,c=15,则a=b=.912练习3、如图，两个正方形的面积分别为64，49，则AC=.ADC644917试一试:815练习4、在△ＡＢＣ中，∠Ｃ＝９０°，ＡＣ＝15，ＣＢ＝20．（1）求△ＡＢＣ的面积ＣＡＢ（2）求斜边ＡＢ（3）求高ＣＤ试一试:Ｄ学习体会1.本节课你又有那些收获？2.预习时的疑难问题解决了吗？你还有那些疑惑？3.你认为本节还有哪些需要注意的地方？2、查阅有关勾股定理的历史资料，及证明方法，与同学交流。1、课本28页，第1、2、3题；课后作业