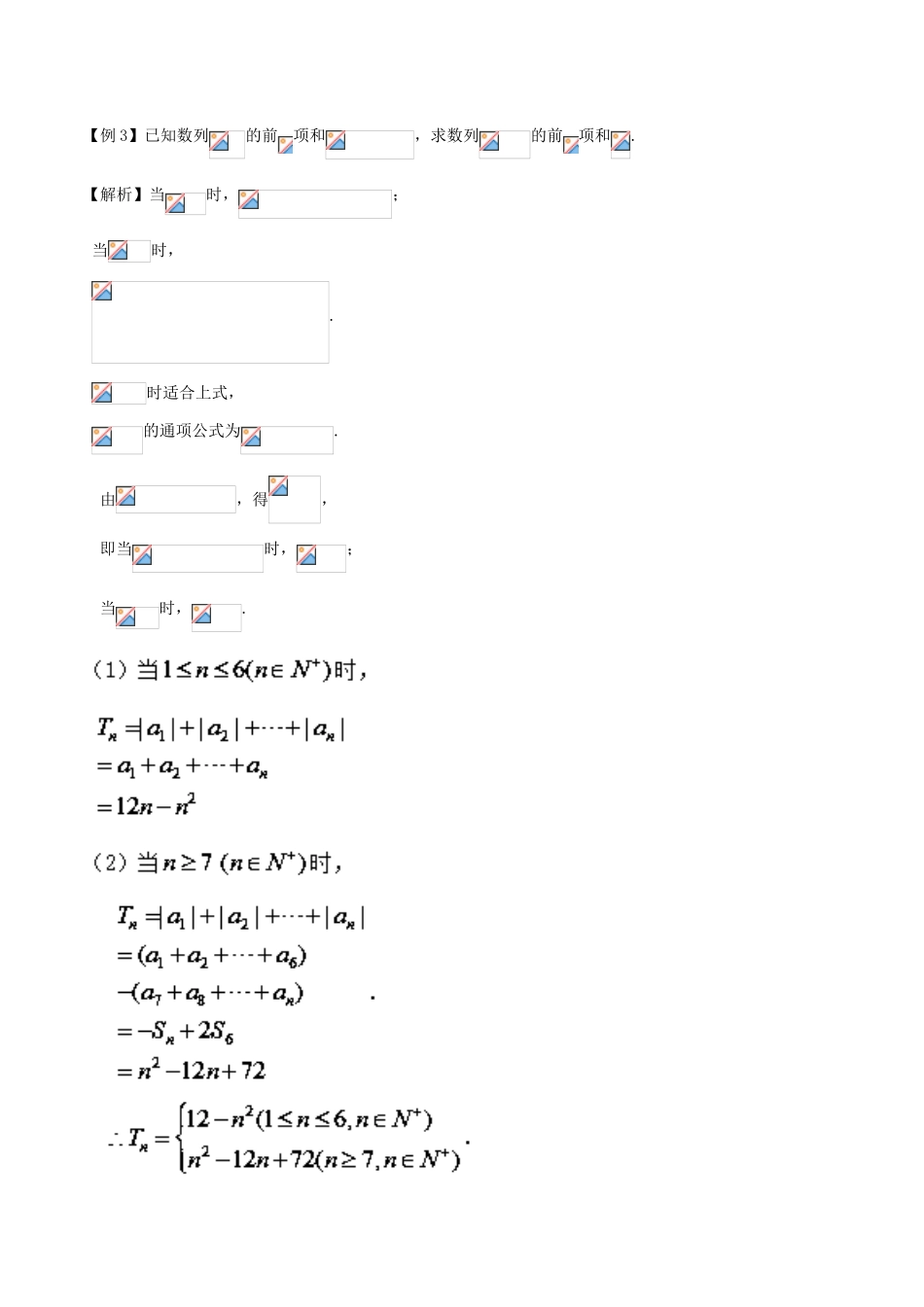
第38讲等差等比数列的性质【知识要点】一、等差数列的通项公式它是一个一次函数;等比数列的通项公式:.二、等差数列的前项和公式:一般已知时,用公式,已知时,用公式由于其常数项为零,所以其图像过原点.等比数列的前项和公式:.三、等差数列中,如果,则,特殊地,时,则,是的等差中项.等比数列中,如果,则,特殊地,时,则,是的等比中项.四、等差数列被均匀分段求和后,得到的数列仍是等差数列,即成等差数列.等比数列被均匀分段求和后,得到的数列仍是等比数列,即成等比数列.【方法讲评】性质一等差数列的通项公式等比数列的通项公式:【例1】已知等差数列中,,求.【点评】对于等差数列的性质要注意灵活运用,提高解题效率.知道了等差数列中的两项,就可以求出数列的公差.等差数列的首项是相对的,可以把其中的某些项看作是首项.【例2】已知等比数列中,求的值.【点评】对于等比数列的通项,要灵活运用,等比数列的首项是相对的,可以选取恰当的项作为等比数列的首项,提高解题效率.【反馈检测1】已知等比数列满足,且是与的等差中项.求数列的通项公式.性质二等差数列的前项和公式:等比数列的前项和公式:【例3】已知数列的前项和,求数列的前项和.【解析】当时,;当时,.时适合上式,的通项公式为.由,得,即当时,;当时,.【点评】(1)已知,一般利用作差法.(2)由于的不确定性,所以需要讨论.【反馈检测2】设数列各项为正数,且.(Ⅰ)证明:数列为等比数列;(Ⅱ)设数列的前项和为,求使成立时的最小值.性质三等差数列中,如果,则,特殊地,时,则,是的等差中项.等比数列中,如果,则,特殊地,时,则,是的等比中项.【例4】已知为等差数列,++=105,=99,以表示的前项和,求使得达到最大值的的值.【点评】当数列中出现了较多的项的关系式时,注意观察它们之间和的关系,看是否能利用等差数列的性质,优化计算,提高解题效率.【例5】等比数列的各项为正数,,则()A.B.C.D.【解析】【点评】当数列中出现了较多的项的关系式时,注意观察它们之间的关系,看是否能利用等差等比数列的性质,优化计算,提高解题效率.【反馈检测3】已知等差数列的前项和为,,,等比数列中,,,则。A.B.C.D.无法确定性质四等差数列被均匀分段求和后,得到的数列仍是等差数列,即成等差数列.等比数列被均匀分段求和后,得到的数列仍是等比数列,即成等比数列.【例6】已知等差数列的前项和为,且,,试求.【点评】解答是依据等差数列均匀分段求和后组成的数列仍为等差数列;熟记等差数列的这些性质常可达到简化解题的目的.【反馈检测4】已知等比数列中,求的值.高中数学常见题型解法归纳及反馈检测第38讲:等差等比数列的性质参考答案【反馈检测1答案】【反馈检测2详细解析】设等比数列的公比为,则有①②由①得:解得或(不合题意舍去).当时,代入②得.【反馈检测2答案】(Ⅰ)证明见解析;(Ⅱ).【反馈检测3答案】【反馈检测3详细解析】由题得所以,故选A.【反馈检测4答案】【反馈检测4详细解析】