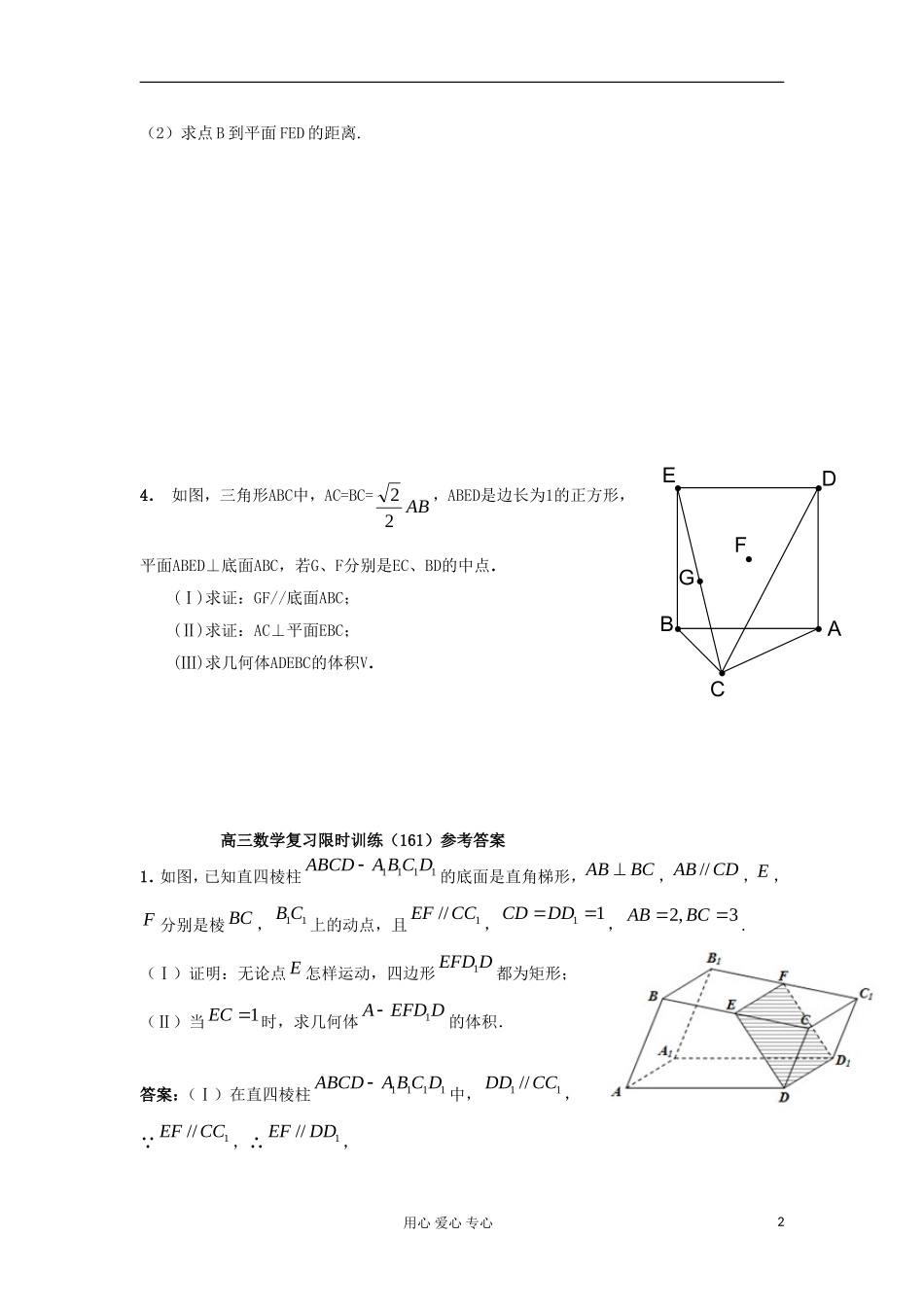
高三数学复习限时训练(166)1.如图,已知直四棱柱1111ABCDABCD的底面是直角梯形,ABBC,//ABCD,E,F分别是棱BC,11BC上的动点,且1//EFCC,11CDDD,2,3ABBC.(Ⅰ)证明:无论点E怎样运动,四边形1EFDD都为矩形;(Ⅱ)当1EC时,求几何体1AEFDD的体积.2、.在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.(1)判别MN与平面AEF的位置关系,并给出证明;(2)求多面体E-AFMN的体积.3.如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC平面BED,FB=a5(1)证明:EBFD用心爱心专心1MNFEBCADAEFMNBFGBDEAC(2)求点B到平面FED的距离.4.如图,三角形ABC中,AC=BC=AB22,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.(Ⅰ)求证:GF//底面ABC;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.高三数学复习限时训练(161)参考答案1.如图,已知直四棱柱1111ABCDABCD的底面是直角梯形,ABBC,//ABCD,E,F分别是棱BC,11BC上的动点,且1//EFCC,11CDDD,2,3ABBC.(Ⅰ)证明:无论点E怎样运动,四边形1EFDD都为矩形;(Ⅱ)当1EC时,求几何体1AEFDD的体积.答案:(Ⅰ)在直四棱柱1111ABCDABCD中,11//DDCC,∵1//EFCC,∴1//EFDD,用心爱心专心2又∵平面//ABCD平面1111ABCD,平面ABCD平面1EFDDED,平面1111ABCD平面11EFDDFD,∴1//EDFD,∴四边形1EFDD为平行四边形,∵侧棱1DD底面ABCD,又DE平面ABCD内,∴1DDDE,∴四边形1EFDD为矩形;(Ⅱ)证明:连结AE,∵四棱柱1111ABCDABCD为直四棱柱,∴侧棱1DD底面ABCD,又AE平面ABCD内,∴1DDAE,在RtABE中,2AB,2BE,则22AE;在RtCDE中,1EC,1CD,则2DE;在直角梯形中ABCD,22()10ADBCABCD;∴222AEDEAD,即AEED,又∵1EDDDD,∴AE平面1EFDD;由(Ⅰ)可知,四边形1EFDD为矩形,且2DE,11DD,∴矩形1EFDD的面积为112EFDDSDEDD,∴几何体1AEFDD的体积为11114222333AEFDDEFDDVSAE.2.在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.(1)判别MN与平面AEF的位置关系,并给出证明;(2)求多面体E-AFMN的体积.答案:(1)因翻折后B、C、D重合(如图),所以MN应是的一条中位线,则用心爱心专心3MNFEBCADAEFMNB.(2)因为平面BEF,且,∴,又∴.3.如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC平面BED,FB=a5(1)证明:EBFD(2)求点B到平面FED的距离.答案:(1)证明:点E为弧AC的中点又又(2)解:在由于:所以用心爱心专心4FGBDEAC由等体积法可知:即,所以即点B到平面FED的距离为4.如图,三角形ABC中,AC=BC=AB22,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.(Ⅰ)求证:GF//底面ABC;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.答案:(I)证法一:取BE的中点H,连结HF、GH,(如图)∵G、F分别是EC和BD的中点∴HG//BC,HF//DE,又∵ADEB为正方形∴DE//AB,从而HF//AB∴HF//平面ABC,HG//平面ABC,HF∩HG=H,∴平面HGF//平面ABC∴GF//平面ABC证法二:取BC的中点M,AB的中点N连结GM、FN、MN(如图)∵G、F分别是EC和BD的中点∴DANFDA,NFBE,GMBEGM21//21,//且且又∵ADEB为正方形∴BE//AD,BE=AD∴GM//NF且GM=NF∴MNFG为平行四边形∴GF//MN,又ABCMN平面,∴GF//平面ABC证法三:连结AE,∵ADEB为正方形,∴AE∩BD=F,且F是AE中点,∴GF//AC,又AC平面ABC,∴GF//平面ABC用心爱心专心5NMFGBDEACHFGBDEACAEFMNB(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF//平面ABC又∵平面ABED⊥平面ABC,∴BE⊥平面ABC∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC,∵BC∩BE=B,∴AC⊥平面BCE(Ⅲ)连结CN,因为AC=BC,∴CN⊥AB,又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED.∵三角形ABC是等腰直角三角形,∴1122CNAB,∵C—ABED是四棱锥,∴VC—ABED=13ABEDSCN用心爱心专心6