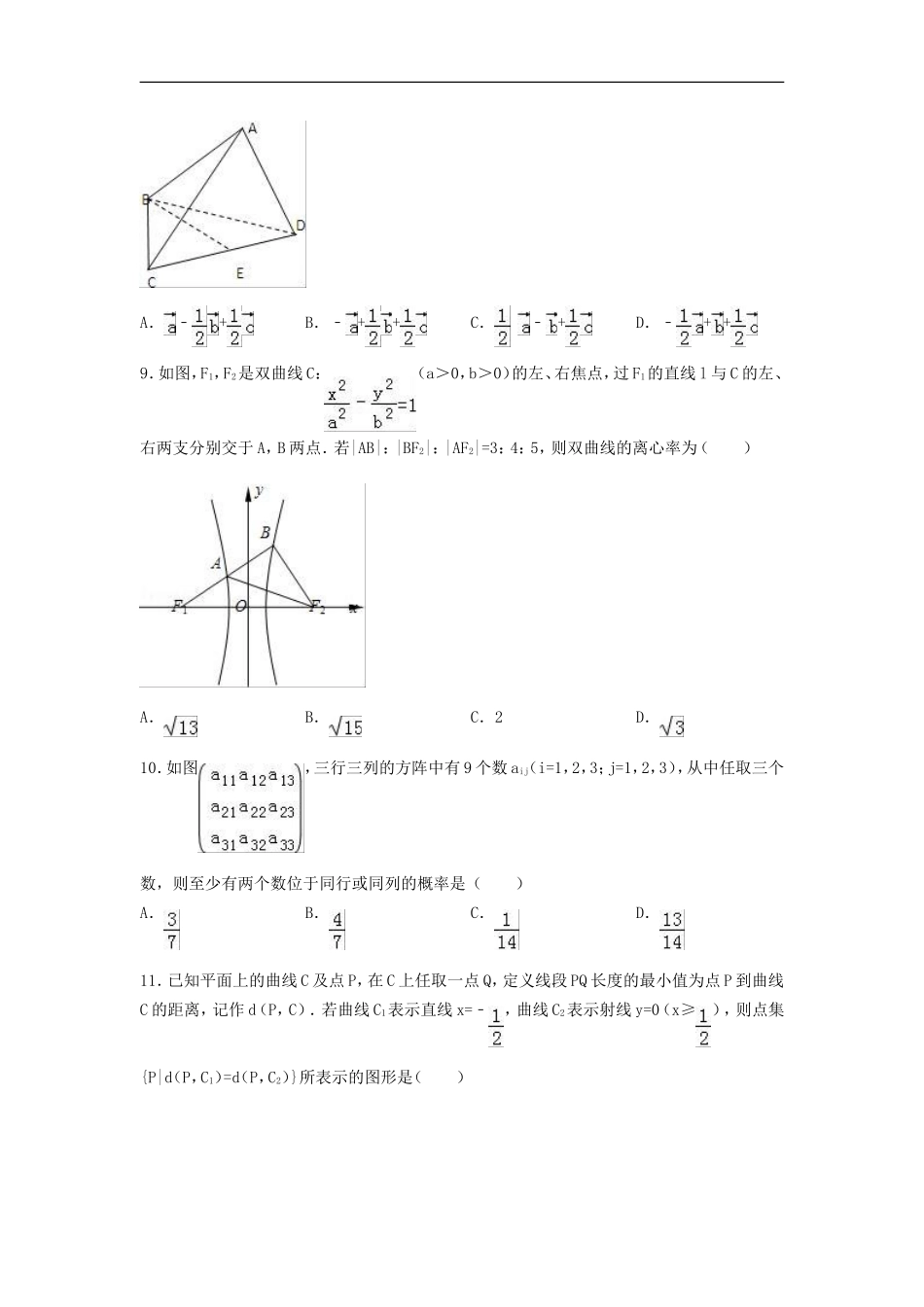
2015-2016学年湖北省武汉市黄陂一中高二(上)12月月考数学试卷(理科)一、选择题(每小题5分,共60分)1.命题“∀x∈R,x2﹣2x+4≤0”的否定为()A.∀x∈R,x2﹣2x+4≥0B.∃x∈R,x2﹣2x+4>0C.∀x∉R,x2﹣2x+4≤0D.∃x∉R,x2﹣2x+4>02.双曲线的离心率大于的必要不充分条件是()A.B.1<m<2C.m>1D.0<m<13.已知双曲线x2﹣ky2=1的一个焦点是,则其渐近线的方程为()A.B.y=±4xC.D.y=±2x4.已知抛物线y2=4x的准线与双曲线交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则a的值为()A.B.C.D.5.若的展开式中含有常数项,则正整数n的最小值是()A.4B.5C.6D.76.5人站成一排,甲、乙两人之间恰有1人的不同站法的种数为()A.18B.24C.36D.487.用一个边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢.现将半径为1的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为()A.B.C.D.8.如图,四面体ABCD中,点E是CD的中点,记,,,则=()A.﹣+B.﹣++C.﹣+D.﹣++9.如图,F1,F2是双曲线C:(a>0,b>0)的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为()A.B.C.2D.10.如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则至少有两个数位于同行或同列的概率是()A.B.C.D.11.已知平面上的曲线C及点P,在C上任取一点Q,定义线段PQ长度的最小值为点P到曲线C的距离,记作d(P,C).若曲线C1表示直线x=﹣,曲线C2表示射线y=0(x≥),则点集{P|d(P,C1)=d(P,C2)}所表示的图形是()A.B.C.D.12.在平面直角坐标系中,A(﹣1,0),B(1,0),若曲线C上存在一点P,使∠APB为钝角,则称曲线上有钝点,下列曲线中“有钝点的曲线”是()①x2=4y;②;③x2﹣y2=1;④(x﹣2)2+(y﹣2)2=4;⑤3x+4y=4.A.①②④B.①②⑤C.①④⑤D.①③④二、填空题(每小题5分,共20分)13.已知的展开式中x3的系数为,则常数a的值为.14.过点的双曲线C的渐近线方程为,P为双曲线C右支上一点,F为双曲线C的左焦点,点A(0,3),则|PA|+|PF|的最小值为.15.“渐升数”是指每个数字比它左边的数字大的正整数(如1468),若把四位“渐升数”按从小到大的顺序排列,则第30个数为.16.已知曲线C:,给出以下结论:①垂直于x轴的直线与曲线C只有一个交点②直线y=kx+m(k,m∈R)与曲线C最多有三个交点③曲线C关于直线y=﹣x对称④若P1(x1,y1),P2(x2,y2)为曲线C上任意两点,则有写出正确结论的序号.三.解答题:(本大题共6小题,共70分)17.已知命题p:点M(1,3)不在圆(x+m)2+(y﹣m)2=16的内部,命题q:“曲线表示焦点在x轴上的椭圆”,命题s:“曲线表示双曲线”.(1)若“p且q”是真命题,求m的取值范围;(2)若¬s是¬q的必要不充分条件,求t的取值范围.18.有5个不同的球,5个不同的盒子,现要把球全部放入盒内.(1)共有几种放法?(2)恰有一个盒子不放球,共有几种放法?(3)恰有两个盒子不放球,共有几种放法?19.已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)求证:BN⊥平面C1B1N;(2)设θ为直线C1N与平面CNB1所成的角,求sinθ的值;(3)设M为AB中点,在BC边上求一点P,使MP∥平面CNB1,求的值.20.已知关于x的一次函数y=ax+b,(1)设集合P={﹣2,﹣1,1,2,3}和Q={﹣2,0,3},分别从集合P和Q中随机取一个数作为a和b,求函数y=ax+b是增函数的概率;(2)实数a,b满足条件求函数y=ax+b的图象经过二、三、四象限的概率.21.已知椭圆C:=1,过点P(4,0)且不垂直于x轴的直线l与曲线C相交于A,B两点.(1)求的取值范围;(2)若B点关于x轴的对称点为E点,探索直线AE与x轴的相交点是否为定点.22.已知动圆P过定点A(﹣3,0),且与圆B:(x﹣3)2+y2=64相切,点P的轨迹为曲线C;设Q为曲线C上(不在x轴上)的动点,过点A作OQ的平行线交曲线C于M,N两点.(Ⅰ)求曲线C的方程;(Ⅱ)是否存在常数λ,使=λ2总成立,...