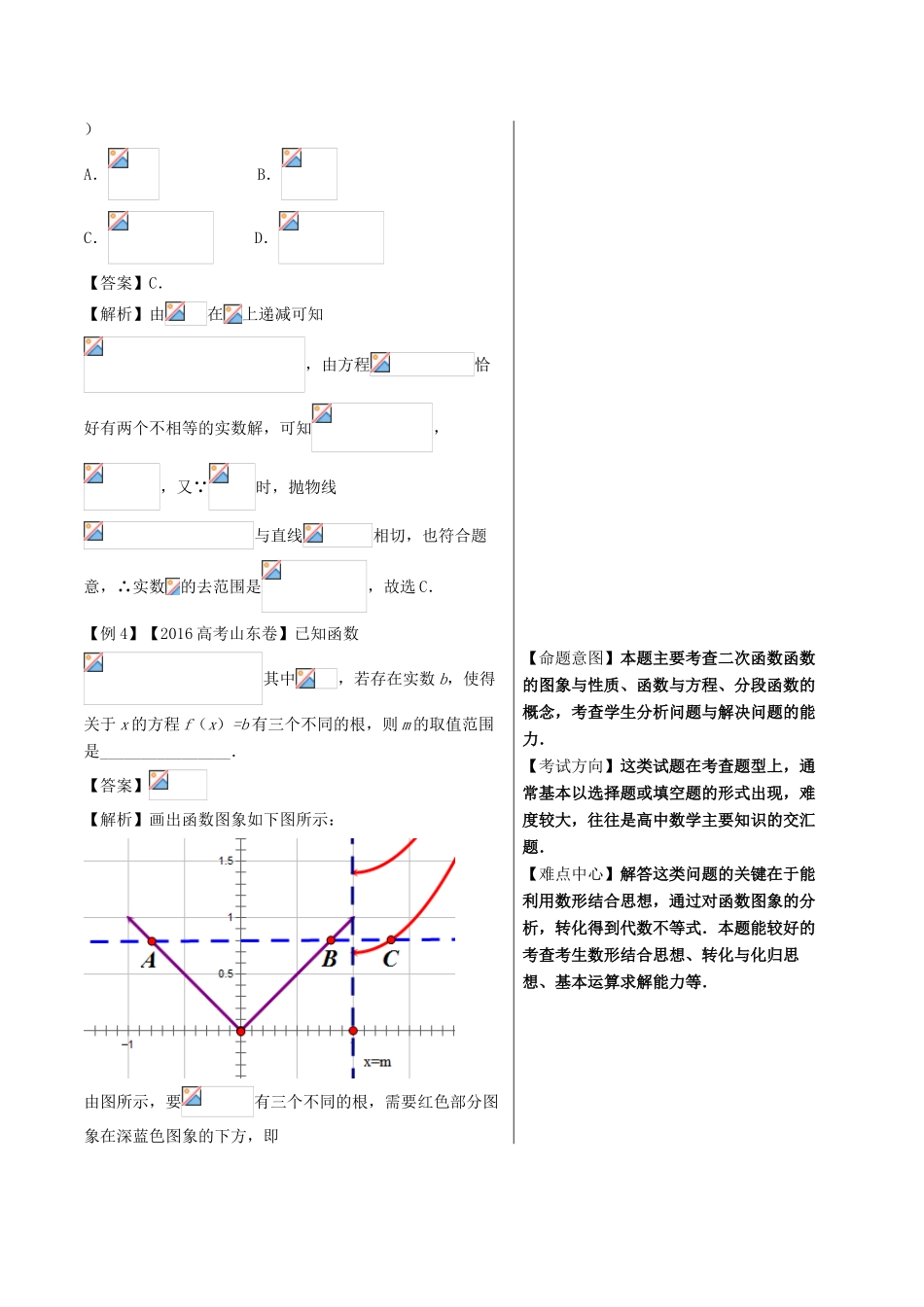
第21题函数零点的性质问题I.题源探究·黄金母题【例1】求函数的零点的个数.【答案】1.【解析】的定义域为.由零点存在性定理知有零点.又在上是单调递增函数,只有一个零点.精彩解读【试题来源】人教版A版必修1P88例1.【母题评析】本题考查了零点存在性定理、函数零点个数的判断.【思路方法】判断函数是否存在零点可用零点存在性定理或利用数形结合法.而要判断函数有几个零点,还需要借助函数的单调性.II.考场精彩·真题回放【例2】【2017高考山东卷】已知当时,函数的图象与的图象有且只有一个交点,则正实数的取值范围是()A.B.C.D.【答案】B【解析】当时,,单调递减,且,单调递增,且,此时有且仅有一个交点;当时,,在上单调递增,所以要有且仅有一个交点,需,故选B.【例3】【2016高考天津卷】已知函数f(x)=(a>0,且a≠1)在R上单调递减,且关于x的方程恰好有两个不相等的实数解,则a的取值范围是(【命题意图】本题主要考查分段函数的零点问题.本题能较好的考查考生分析问题、解决问题的能力,以及数形结合、转化与化归能力等.【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较大.【难点中心】已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.)A.B.C.D.【答案】C.【解析】由在上递减可知,由方程恰好有两个不相等的实数解,可知,,又 时,抛物线与直线相切,也符合题意,∴实数的去范围是,故选C.【例4】【2016高考山东卷】已知函数其中,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是________________.【答案】【解析】画出函数图象如下图所示:由图所示,要有三个不同的根,需要红色部分图象在深蓝色图象的下方,即【命题意图】本题主要考查二次函数函数的图象与性质、函数与方程、分段函数的概念,考查学生分析问题与解决问题的能力.【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,难度较大,往往是高中数学主要知识的交汇题.【难点中心】解答这类问题的关键在于能利用数形结合思想,通过对函数图象的分析,转化得到代数不等式.本题能较好的考查考生数形结合思想、转化与化归思想、基本运算求解能力等.,解得.III.理论基础·解题原理函数零点、方程的根、函数图象交点的相互转化:有关零点个数及性质的问题会用到这三者的转化,且这三者各具特点:(1)函数的零点:有“零点存在性定理”作为理论基础,可通过区间端点值的符号和函数的单调性确定是否存在零点;(2)方程的根:方程的特点在于能够进行灵活的变形,从而可将等号两边的表达式分别构造为两个可分析的函数,为作图做好铺垫;(3)函数图象的交点:通过作图可直观的观察到交点的个数,并能初步判断交点所在区间.三者转化:函数的零点方程的根方程的根函数与的交点.IV.题型攻略·深度挖掘【考试方向】这类试题在考查题型上,通常基本以选择题或填空题的形式出现,一般综合性较强,难度较大.【技能方法】1.已知函数有零点求参数取值范围常用的方法:(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.2.此类问题的处理步骤:(1)作图:可将零点问题转化成方程,进而通过构造函数将方程转化为两个图象交点问题,并作出函数图象;(2)确定变量范围:通过图象与交点位置确定参数和零点的取值范围;(3)观察交点的特点(比如对称性等)并选择合适的方法处理表达式的值.【易错指导】对函数零点存在的判断需要注意以下两点:(1)函数在上连续;(2)满足.上述方法只能求变号零点,对于非变号零点不能用上述方法求解.另外需要注意的是:(1)若...