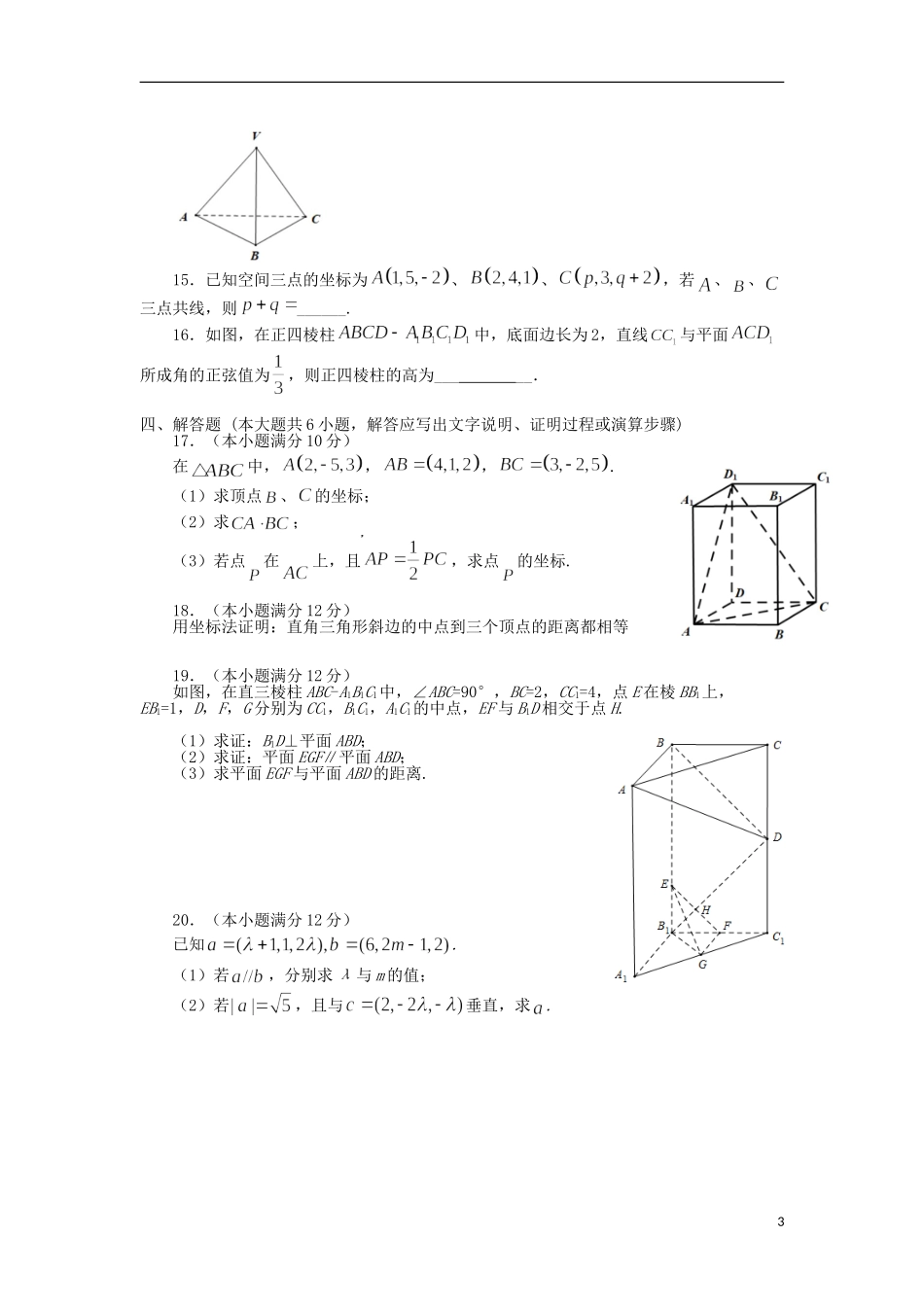
辽宁省大连市瓦房店市实验高级中学2020-2021学年高二数学上学期月考试题时间:120分钟满分:150分一、单选题(本大题共8小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题中,假命题是()A.同平面向量一样,任意两个空间向量都不能比较大小B.两个相等的向量,若起点相同,则终点也相同C.只有零向量的模等于0D.共线的单位向量都相等2.设,向量,∥,则()A.B.C.3D.43.若直线l∥α,且l的方向向量为(2,m,1),平面α的法向量为,则m为()A.-4B.-6C.-8D.84.在长方体中,,,则直线与平面所成角的正弦值为()A.B.C.D.5.已知平面的一个法向量为,点在平面内,则点到平面的距离为()A.B.C.1D.6.如图,二面角--为60°,A、B是棱上的两点,、分别在半平面内,,,且,,则的长为()A.B.C.D.7.在四面体O-ABC中,G1是△ABC的重心,G是OG1上的一点,且OG=3GG1,若=x+y+z,则(x,y,z)为()A.B.C.D.8.在空间直角坐标系中,,为的中点,1为空间一点且满足,若,,则()A.9B.7C.5D.3二、多选题(本大题共4小题,每小题5分。在每小题给出的四个选项中,至少两个选项正确,选对得5分,少选得3分,错选得0分)9.对于,下列说法正确的是()A.可看作点与点的距离B.可看作点与点的距离C.可看作点与点的距离D.可看作点与点的距离10.关于空间向量,以下说法正确的是()A.空间中的三个向量,若有两个向量共线,则这三个向量一定共面B.若对空间中任意一点,有,则,,,四点共面C.已知向量组是空间的一个基底,若,则也是空间的一个基底D.若,则是钝角11.如图,正方体的棱长为1,是的中点,则()A.直线平面B.C.三棱锥的体积为D.异面直线与所成的角为12.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,下列说法中正确的是()A.B.C.向量与的夹角是60°D.与AC所成角的余弦值为三、填空题(本大题共4小题,每小题5分)13.设点A在x轴上,点B在y轴上,的中点是,则等于________14.如图,正三棱锥的侧棱长为3,底面边长为2,则与所成角的余弦值为______.215.已知空间三点的坐标为、、,若、、三点共线,则______.16.如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为_____.四、解答题(本大题共6小题,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)在中,,,.(1)求顶点、的坐标;(2)求;(3)若点在上,且,求点的坐标.18.(本小题满分12分)用坐标法证明:直角三角形斜边的中点到三个顶点的距离都相等19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在棱BB1上,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.(1)求证:B1D⊥平面ABD;(2)求证:平面EGF∥平面ABD;(3)求平面EGF与平面ABD的距离.20.(本小题满分12分)已知.(1)若,分别求λ与m的值;(2)若,且与垂直,求.321.(本小题满分12分)如图,三棱柱中,平面,点E是棱的中点,已知.(Ⅰ)求证:平面ABC;(Ⅱ)求二面角的余弦值.22.(本小题满分12分)如图,在四棱锥中,底面为直角梯形,,,,,,,平面平面,点在棱上,,分别为的中点,过三点的平面交于点,且平面.(1)求的值;(2)求与平面所成角的正弦值.答案4一、单选题:DCCBABAD二、多选题:BCDABCABDAB三、填空题:054四、解答题:17.(本小题满分10分)(1)设点为坐标原点,,则.,则;…2分(2),则,又,因此,;…6分(3)设点为坐标原点,,则,则,所以,点的坐标为.…10分18.(本小题满分12分)证明:建立如图所示的平面直角坐标系,设,,则AB的中点C的坐标为. ,,5∴,即直角三角形斜边的中点到三个顶点的距离都相等.19.(本小题满分12分)(1)证明:如图所示建立空间直角坐标系,设AB=a,则A1(a,0,0),B1(0,0,0),C1(0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),D(0,2,2),G.所以=(0,2,2),=(-a,0,0),=(0,2,-2).所以=0+0+0=0,=0+4-4=0.所以,所以B1...