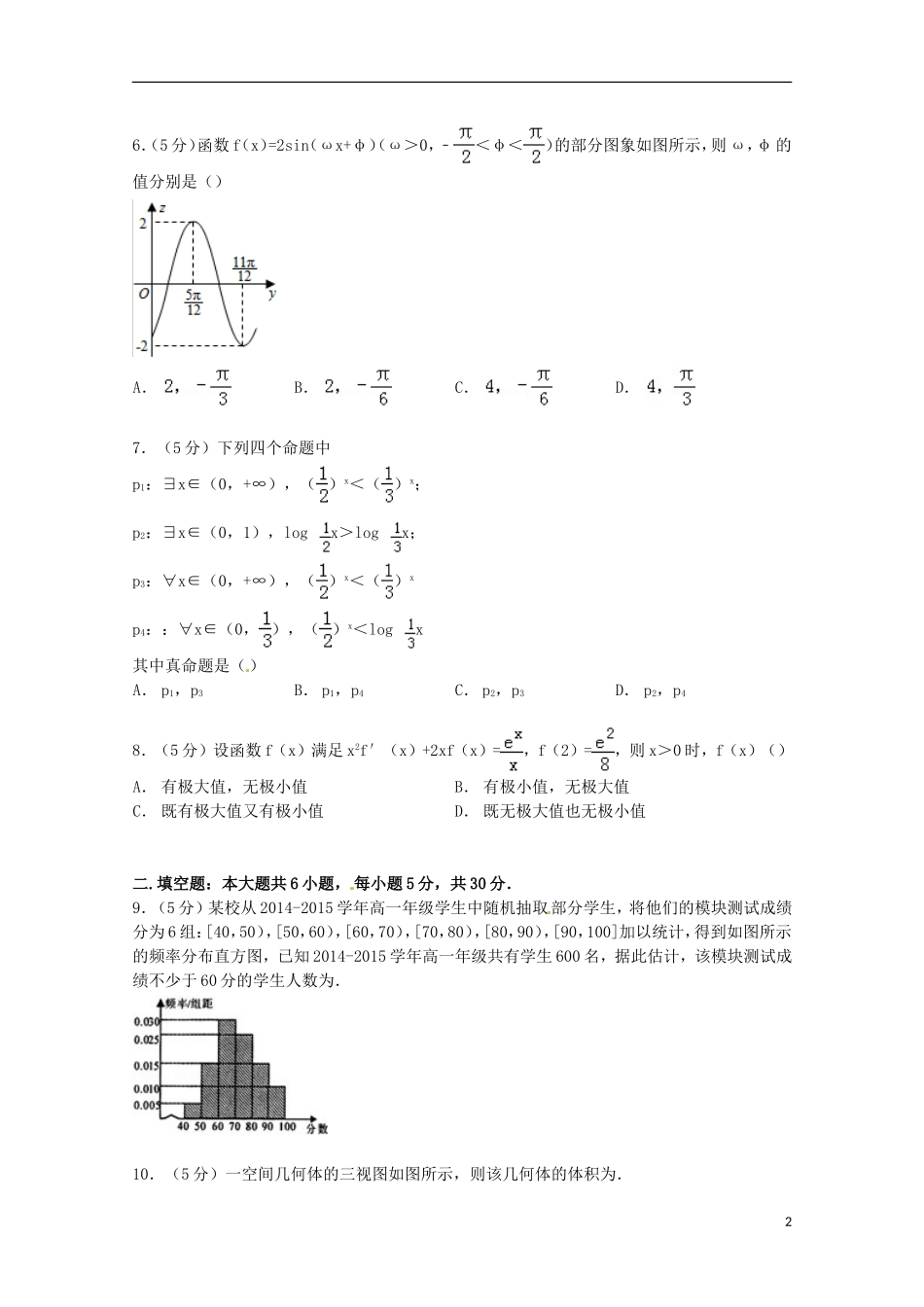
天津市河西区2015届高考数学二模试卷(文科)一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)a为正实数,i是虚数单位,||=2,则a=()A.2B.C.D.12.(5分)设变量x,y满足约束条件,则目标函数z=3x+y的最小值为()A.11B.3C.2D.3.(5分)某程序框图如图所示,若该程序运行后输出的值是,则()A.a=4B.a=5C.a=6D.a=74.(5分)函数f(x)=x2﹣4x﹣2lnx+5的零点个数为()A.3B.2C.1D.05.(5分)已知双曲线﹣=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为,则p=()A.1B.C.2D.316.(5分)函数f(x)=2sin(ωx+φ)(ω>0,﹣<φ<)的部分图象如图所示,则ω,φ的值分别是()A.B.C.D.7.(5分)下列四个命题中p1:∃x∈(0,+∞),()x<()x;p2:∃x∈(0,1),logx>logx;p3:∀x∈(0,+∞),()x<()xp4::∀x∈(0,),()x<logx其中真命题是()A.p1,p3B.p1,p4C.p2,p3D.p2,p48.(5分)设函数f(x)满足x2f′(x)+2xf(x)=,f(2)=,则x>0时,f(x)()A.有极大值,无极小值B.有极小值,无极大值C.既有极大值又有极小值D.既无极大值也无极小值二.填空题:本大题共6小题,每小题5分,共30分.9.(5分)某校从2014-2015学年高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知2014-2015学年高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为.10.(5分)一空间几何体的三视图如图所示,则该几何体的体积为.211.(5分)关于x的不等式x2﹣2ax﹣8a2<0(a>0)的解集为(x1,x2),且x2﹣x1=15,则a=.12.(5分)如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=.13.(5分)已知向量与的夹角为120°,且||=2,||=3,若=λ+,且⊥,则实数λ的值为.14.(5分)已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若同时满足条件:①∀x∈R,f(x)<0或g(x)<0;②∃x∈(﹣∞,﹣4),f(x)g(x)<0.则m的取值范围是.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)若某公司从七位大学毕业生A,B,C,D,E,F,G,中录用两人,这七人被录用的机会均等.(Ⅰ)用题中字母列举出所有可能的结果;(Ⅱ)设事件M为“A或B被录用”求事件M发生的概率.16.(13分)设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c)(a﹣b+c)=ac.(Ⅰ)求B.3(Ⅱ)若sinAsinC=,求C.17.(13分)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)(Ⅰ)当λ=1时,证明:直线BC1∥平面EFPQ;(Ⅱ)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.18.(13分)已知点A(0,﹣2),椭圆E:+=1(a>b>0)的离心率为,F是椭圆E的右焦点,直线AF的斜率为,O为坐标原点.(Ⅰ)求E的方程;(Ⅱ)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.19.(14分)已知函数f(x)=(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.(Ⅰ)求k的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=(x2+x)f′(x),其中f′(x)是f(x)的导函数.证明:对任意x>0,g(x)<1+e﹣2.20.(14分)设数列{an}的前n项和为Sn,已知a1=1,,n∈N*.(1)求a2的值;(2)求数列{an}的通项公式;(3)证明:对一切正整数n,有.天津市河西区2015届高考数学二模试卷(文科)4参考答案与试题解析一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)a为正实数,i是虚数单位,||=2,则a=()A.2B.C.D.1考点:复数代数形式的乘除...