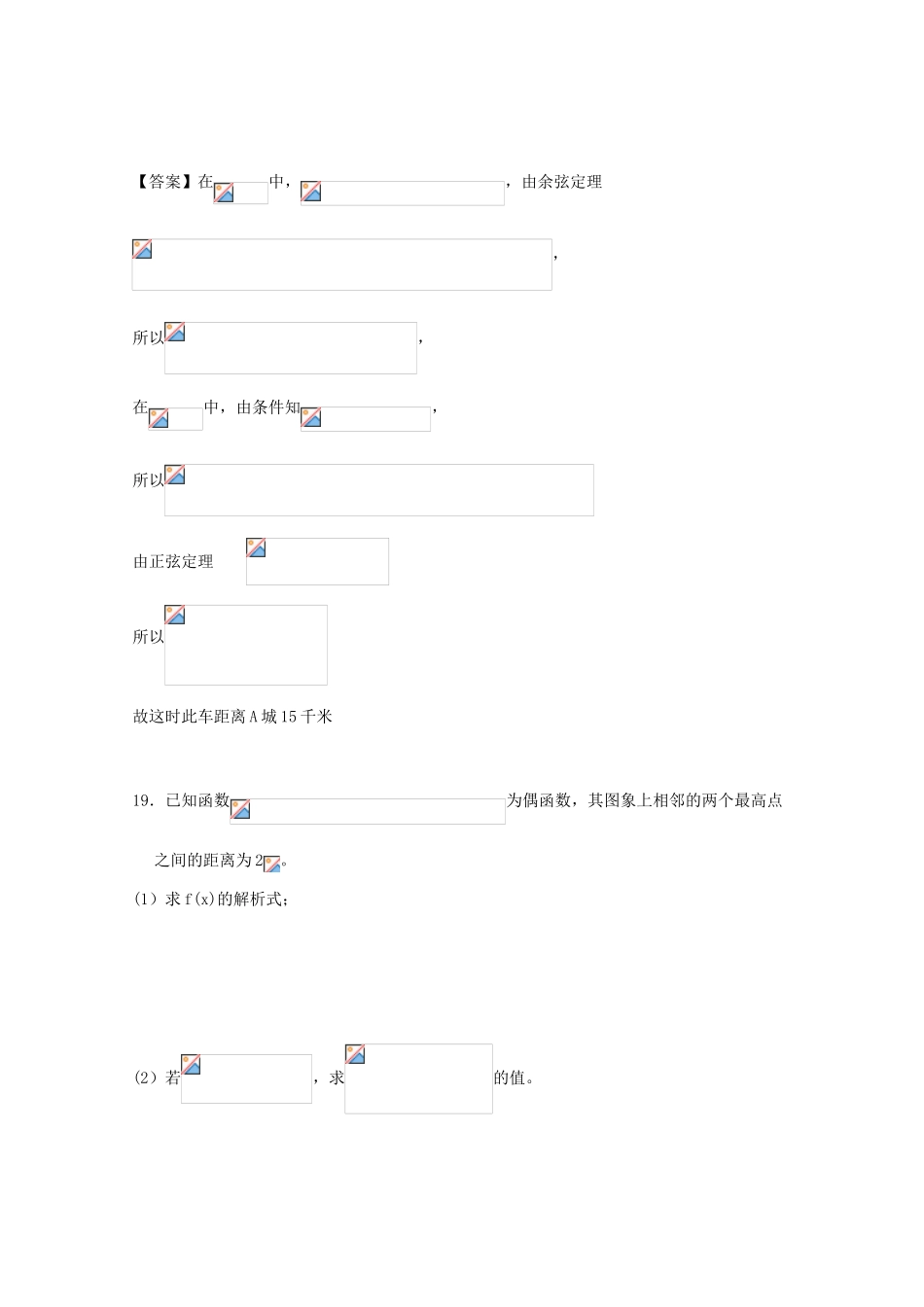
2018高考数学一轮复习三角函数专题检测试题及答案02解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.如图,在半径为、圆心角为的扇形的弧上任取一点,作扇形的内接矩形,使点在上,点在上,设矩形的面积为,(1)按下列要求写出函数的关系式:①设,将表示成的函数关系式;②设,将表示成的函数关系式,(2)请你选用(1)中的一个函数关系式,求出的最大值.【答案】(1)①因为,,所以,所以.②因为,,,所以所以,即,(2)选择,所以.18.如图,某观测站C在城A的南偏西的方向,从城A出发有一条走向为南偏东的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?【答案】在中,,由余弦定理,所以,在中,由条件知,所以由正弦定理所以故这时此车距离A城15千米19.已知函数为偶函数,其图象上相邻的两个最高点之间的距离为2。(1)求f(x)的解析式;(2)若,求的值。【答案】(1)由已知得:∵为偶函数,即∵∴∴(2)由得,则有20.一缉私艇A发现在北偏东方向,距离12nmile的海面上有一走私船C正以10nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14nmile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.【答案】设A,C分别表示缉私艇,走私船的位置,设经过小时后在B处追上,则有,所以所需时间2小时,21.2016年航空航天技术展览会在上海国际展览中心举行,一次飞行表演中,一架直升飞机在海拔800m的高度飞行,从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是和.(Ⅰ)试计算这个海岛的宽度.(Ⅱ)若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为和,他们估计P、Q两处距离大约为600m,由此试估算出观测者甲(在P处)到飞机的直线距离.【答案】(1)在中,,则.在中,,则.所以,(m).(2)在中,,,.根据正弦定理,得,则22.中,内角的对边分别是,已知成等比数列,且.(1)求的值;(2)设,求的值.【答案】(1)由,得由及正弦定理得于是(2)由得由可得,即由余弦定理得